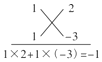题目内容
【题目】在自习课上,小明拿来如下框的一道题目(原问题)和合作学习小组的同学们交流.
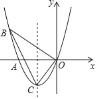
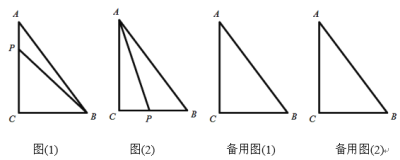
如图1,已知△ABC,∠ACB=90°,∠ABC=45°,分别以AB,BC为边向外作△ABD与△BCE,且DA=DB,EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F.探究线段DF与EF的数量关系.
小红同学的思路是:过点D作DG⊥AB于点G,构造全等三角形,通过推理使问题得解.
小华同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60°.
请你参考小明同学的思路,探究并解决以下问题:
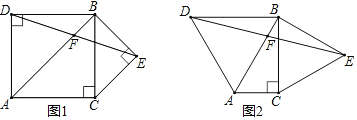
(1)写出原问题中DF与EF的数量关系为 .
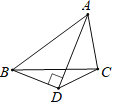
(2)如图2,若∠ABC=30°,∠ADB=∠BEC=60°,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.
【答案】(1)DF=EF;(2)不发生变化,理由见解析
【解析】
(1)结论:DF=EF.只要证明△DFG≌△EFB(AAS)即可解决问题;
(2)猜想:DF=FE.过点D作DG⊥AB于G,则∠DGB=90°.由Rt△DBG≌Rt△BAC(HL),推出DG=BC,再证明△DFG≌△EFB(AAS)即可解决问题;
解:(1)结论:DF=EF.
理由:作DG⊥AB于G.
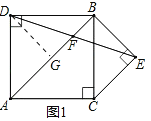
∵∠DBG=∠CBE=45°,∠DGB=∠BEC=90°,DB=BC,
∴△DBG≌△BCE(AAS),
∴GD=BE,
∵∠DGB=∠GBE=90°,
∴DG∥BE,
∴∠FDG=∠BEF,
∵∠DFG=∠BFE,
∴△DFG≌△EFB(AAS),
∴DF=EF.
故答案为DF=EF.
(2)猜想:DF=FE.
理由:过点D作DG⊥AB于G,则∠DGB=90°.
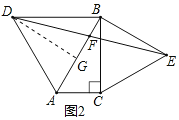
∵DA=DB,∠ADB=60°.
∴AG=BG,△DBA是等边三角形,
∴DB=BA,
∵∠ACB=90°,∠ABC=30°,
∴AC=![]() AB=BG,
AB=BG,
在Rt△DBG和Rt△BAC中,
![]()
∴Rt△DBG≌Rt△BAC(HL),
∴DG=BC,
∵BE=EC,∠BEC=60°,
∴△EBC是等边三角形,
∴BC=BE,∠CBE=60°,
∴DG=BE,∠ABE=∠ABC+∠CBE=90°,
在△DFG和△EFB中,
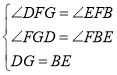
∴△DFG≌△EFB(AAS),
∴DF=EF.

 科学实验活动册系列答案
科学实验活动册系列答案