题目内容
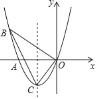
【题目】如图,已知抛物线y=ax2+bx经过点A(﹣2,0)、B(﹣3,3),顶点为C.
(1)求抛物线的函数表达式;
(2)若点P是第一象限内的抛物线上一动点,过点P作PM⊥x轴于点M,则是否存在点P,使得以P、M、A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1) y=x2+2x;(2)见解析.
【解析】
(1)利用待定系数法直接求出抛物线的解析式;(2)分两种情况讨论,①若△AMP∽△BOC,②若△PMA∽△BOC,根据相似三角形对应边的比相等可以求出P点坐标.
解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),且过A(﹣2,0),B(﹣3,3),O(0,0)可得
![]() ,
,
解得:![]() .
.
故抛物线的解析式为:y=x2+2x;
(2)存在,
如图:∵B(﹣3,3),C(﹣1,﹣1),根据勾股定理得:
BO2=18,CO2=2,BC2=20,
∴BO2+CO2=BC2.
∴△BOC是直角三角形.
假设存在点P,使以P,M,A为顶点的 三角形与△BOC相似,
设P(x,y),由题意知x>0,y>0,且y=x2+2x,
①若△AMP∽△BOC,则![]() =
=![]() ,
,
即 x+2=3(x2+2x)
得:x1=![]() ,x2=﹣2(舍去).
,x2=﹣2(舍去).
当x=![]() 时,y=
时,y=![]() ,即P(
,即P(![]() ,
,![]() ).
).
②若△PMA∽△BOC,则![]() =
=![]() ,
,
即:x2+2x=3(x+2)
得:x1=3,x2=﹣2(舍去)
当x=3时,y=15,即P(3,15).
故符合条件的点P有两个,分别是P(![]() ,
,![]() )和(3,15).
)和(3,15).

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间 (小时) | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时数的说法正确的是( )
A. 众数是8 B. 中位数是3 C. 平均数是3 D. 方差是0.34