题目内容
【题目】有些数学题,表面上看起来无从下手,但根据图形的特点,可补全成为特殊的图形,然后根据特殊几何图形的性质去考虑,常常可以获得简捷解法.根据阅读,请解答问题:如图所示,已知△ABC的面积为16cm2,AD平分∠BAC,且AD⊥BD于点D,则△ADC的面积为___________cm2.
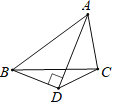
【答案】8
【解析】
延长BD、AC交于点E,由题意证得△ABD≌△AED(ASA),证得AB=AE,BD=DE,即可证得S△ABD=S△AED,S△BDC=S△EDC,设S△EDC=x,利用S△ABE=S△ABC+S△BCD=12+2S△EDC即可求得结果.
解:延长BD、AC交于点E,
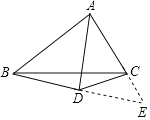
∵AD平分∠BAC,且AD⊥BD于点D,
∴在△ABD和△AED中,
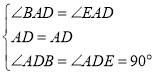
∴△ABD≌△AED(ASA),
∴AB=AE,BD=DE,
∴S△ABD=S△AED,S△BDC=S△EDC,
设S△EDC=x,
∵△ABC的面积为16cm2,
∴S△ABE=S△ABC+S△BCD=16+2S△EDC=16+2x,
∴S△ADC=S△ADE﹣S△EDC=![]()
故答案为8.

练习册系列答案
相关题目