题目内容
【题目】阅读与思考
x2+(p+q)x+pq型式子的因式分解
x2+(p+q)x+pq型式子是数学学习中常见的一类多项式,如何将这种类型的式子分解因式呢?
我们通过学习,利用多项式的乘法法则可知:(x+p)(x+q)=x2+(p+q)x+pq,因式分解是整式乘法相反方向的变形,利用这种关系可得x2+(p+q)x+pq=(x+p)(x+q).
利用这个结果可以将某些二次项系数是1的二次三项式分解因式,例如,将x2﹣x﹣6分解因式.这个式子的二次项系数是1,常数项﹣6=2×(﹣3),一次项系数﹣1=2+(﹣3),因此这是一个x2+(p+q)x+pq型的式子.所以x2﹣x﹣6=(x+2)(x﹣3).
上述过程可用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数,如图所示.
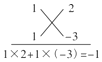
这样我们也可以得到x2﹣x﹣6=(x+2)(x﹣3).这种分解二次三项式的方法叫“十字相乘法”.
请同学们认真观察,分析理解后,解答下列问题:
(1)分解因式:y2﹣2y﹣24.
(2)若x2+mx﹣12(m为常数)可分解为两个一次因式的积,请直接写出整数m的所有可能值.
【答案】(1)(y+4)(y﹣6);(2)﹣1,1,﹣4,4,11,﹣11
【解析】
(1)直接利用十字相乘法分解因式得出答案;
(2)利用十字相乘法分解因式得出所有的可能.
解:(1)y2﹣2y﹣24=(y+4)(y﹣6);
(2)若![]() ,此时
,此时![]()
若![]() ,此时
,此时![]()
若![]() ,此时
,此时![]()
若![]() ,此时
,此时![]()
若![]() ,此时
,此时![]()
![]() ,此时
,此时![]()
综上所述,若x2+mx﹣12(m为常数)可分解为两个一次因式的积,
m的值可能是﹣1,1,﹣4,4,11,﹣11.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目