题目内容
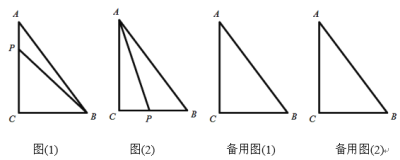
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若动点P从点A开始沿着
,若动点P从点A开始沿着![]() 的路径运动,且速度为每秒2cm,设点P运动的时间为t秒.
的路径运动,且速度为每秒2cm,设点P运动的时间为t秒.
(1)当![]() 时,
时,![]() 的面积是___________
的面积是___________![]() ;
;
(2)如图(2)当t为何值时,AP平分![]() ;
;
(3)当t为何值时,![]() 为等腰三角形.
为等腰三角形.
【答案】(1)45;(2)![]() ;(3)t=2.5秒或25或26.5或23.75.
;(3)t=2.5秒或25或26.5或23.75.
【解析】
(1)当t=3时,求出AP的长,再根据三角形面积公式即可得出结果;
(2)作PD⊥AB于D,由勾股定理求出AB的长,由角平分线性质得出PD=PC=2t-20(cm),AD=AC=20cm,求出BD的长,得出PB=BC-PC=35-2t(cm),在Rt△PBD中,由勾股定理求出t的值即可;
(3)由于点P是动点,故应分点P在AC上与AB上两种情况进行讨论,根据等腰三角形的性质和相似三角形的判定与性质即可得出结果.
(1)当t=3时,AP=2×3=6(cm),
△ABP的面积=![]() AP×BC=
AP×BC=![]() ×6×15=45(cm2);
×6×15=45(cm2);
故答案为:45cm2;
(2)作PD⊥AB于D,如图2所示:
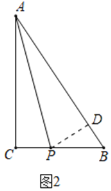
∵在△ABC中,∠C=90°,AC=20cm,BC=15cm,
∴AB=![]() (cm),
(cm),
∵AP平分∠CAB,
∴PD=PC=2t-20(cm),AD=AC=20cm,
∴BD=AB-AD=5cm,
∴PB=BC-PC=15-(2t-20)=35-2t(cm),
在Rt△PBD中,由勾股定理得:BD2+PD2=PB2,
即52+(2t-20)2=(35-2t)2,
解得:t=![]() ,
,
∴当t为![]() 时,AP平分∠CAB;
时,AP平分∠CAB;
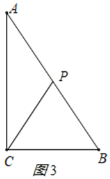
(3)当点P在AC上时,CP=CB=15cm,
∴AP=AC-CP=5cm,
∴t=2.5秒;
当点P在AB上时,分三种情况:
若BP=BC=15cm,t=(20+15+15)÷2=25(秒);
若CP=BC=15cm,
作CM⊥AB,则BM=PM,
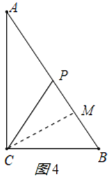
∵∠B=∠B,∠BMC=∠BCA,
∴△ABC∽△CBM,
∴![]() ,即
,即![]() ,
,
解得:CM=12cm,BM=9cm,
∴PB=2BM=18cm,
∴t=(20+15+18)÷2=26.5(秒);
若PC=PB,则∠B=∠BCP,
∵∠B+∠A=90°,∠BCP+∠ACP=90°,
∴∠A=∠ACP,
∴AP=CP=BP=![]() AB=12.5cm,
AB=12.5cm,
∴t=(20+15+12.5)÷2=23.75(秒);
综上所述,当t=2.5秒或25或26.5或23.75秒时,△BCP为等腰三角形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案