题目内容
【题目】如图,在△ABC中,∠ACB=90°,∠A>∠B.
(1)利用尺规作图在BC边上找一点P,使得点P到AB的距离等于PC的长度(不写作法,保留作图痕迹);
(2)在(1)的条件下,如果点P恰好又在线段AB的垂直平分线上,求∠B的度数.
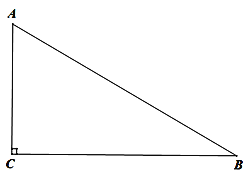
【答案】(1)作图见解析;(2)30°.
【解析】试题分析:(1)因为角平分线上的点到角两边的距离相等,所以要在BC上找一点P,使得点P到AB的距离等于PC的长度,则作角∠BAC的角平分线,角平分线与BC的交点即所求点P,(2)利用垂直平分线的性质可得:PA=PB,所以∠B=∠PAB,又因为(1)中AP是∠BAC的角平分线,所以∠B=∠PAB=![]() ∠BAC,因为∠BAC+∠B=90°,所以3∠B=90°,即∠B=30°.
∠BAC,因为∠BAC+∠B=90°,所以3∠B=90°,即∠B=30°.
试题解析:(1)如图所示,
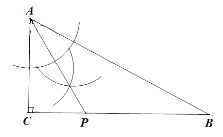
(2) 因为(1)中AP是∠BAC的角平分线,
所以∠PAB=![]() ∠BAC,即∠BAC=2∠PAB,
∠BAC,即∠BAC=2∠PAB,
又因为点P在线段AB的垂直平分线上,
所以PA=PB,
所以∠B=∠PAB,即∠BAC=2∠B,
又因为∠BAC+∠B=90°,
所以3∠B=90°,即∠B=30°.
点睛:本题主要考查角平分线的性质和垂直平分线的性质,解决本题的关键是能够熟练利用角平分线的性质和垂直平分线的性质.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目