��Ŀ����
����Ŀ�����κ���y=![]() +bx+c��a��0���Ķ���ΪP����ͼ����x������������A����m��0����B��1��0������y���ڵ�C��0����3am+6a��������˵������m=3��������APB=120��ʱ��a=
+bx+c��a��0���Ķ���ΪP����ͼ����x������������A����m��0����B��1��0������y���ڵ�C��0����3am+6a��������˵������m=3��������APB=120��ʱ��a=![]() ��������APB=120��ʱ���������ϴ��ڵ�M��M��P���غϣ���ʹ����ABM�Ƕ���Ϊ120��ĵ��������Σ����������ϴ��ڵ�N������ABNΪֱ��������ʱ����a��
��������APB=120��ʱ���������ϴ��ڵ�M��M��P���غϣ���ʹ����ABM�Ƕ���Ϊ120��ĵ��������Σ����������ϴ��ڵ�N������ABNΪֱ��������ʱ����a��![]() .��ȷ���ǣ� ��.
.��ȷ���ǣ� ��.
A���٢� B���ۢ� C���٢ڢ� D���٢ڢۢ�
���𰸡�D.
��������
�������������A��B���������ֱ���������ߵĽ���ʽ�õ�![]() ��ʽ��a+b+c=0��ʽ������ʽ������ɵõ�m=
��ʽ��a+b+c=0��ʽ������ʽ������ɵõ�m=![]() �����ɵõ�C��0��3a��3b�����Ӷ��õ�c=3a��3b��������ʽ�ɵ�b=2a������m=
�����ɵõ�C��0��3a��3b�����Ӷ��õ�c=3a��3b��������ʽ�ɵ�b=2a������m=![]() =3��������ȷ��
=3��������ȷ��
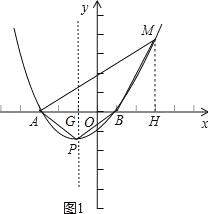
����m=3����A����3��0�����������ߵĽ���ʽ����Ϊy=a��x+3����x��1�����ɵ�����P������Ϊ����1����4a�������ݶԳ��Կɵ�PA=PB�����PAB=��PBA=30�㣮�������ߵĶԳ�����x��Ľ���ΪG������PG��x�ᣬ��PG=AGtan��PAG=2��![]() =
=![]() ����4a=
����4a=![]() ����a=
����a=![]() ��������ȷ��
��������ȷ��
���ڵ�һ����������MBA=120�㣬������BM=BA������M��MH��x����H����ͼ1����Rt��MHB�У���MBH=60�㣬����MH=4sin60��=4��![]() =
=![]() ��BH=4cos60��=4��
��BH=4cos60��=4��![]() =2������M��������3��
=2������M������Ϊ��3��![]() ������x=3ʱ��y=
������x=3ʱ��y=![]() ��3+3����3��1��=
��3+3����3��1��=![]() ������M���������ϣ�������ȷ��
������M���������ϣ�������ȷ��
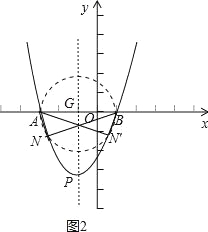
������N���������ϣ����ABN��90�㣬��BAN��90�㣮����ABNΪֱ��������ʱ����ANB=90�㣬��ʱ��N����ABΪֱ������G�ϣ������N����G�������ߵĽ��㴦��Ҫʹ��N���ڣ���P��������G�ϻ���G�⣬��ͼ2������PG��2����4a��2��Ҳ��a��![]() ��������ȷ��
��������ȷ��
��ѡ��D��