题目内容
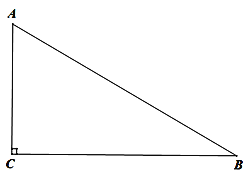
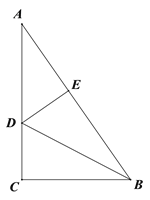
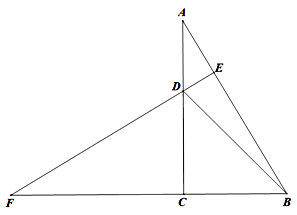
【题目】如图,Rt△ABC中,∠ACB=90°,D为AC上一动点(不与点A、C重合),过D作DE⊥AB于E.
(1)当BD平分∠ABC时
①若AC=8,BC=6,求线段AE的长度;
②在①的条件下,求△ADB的面积;
(2)延长BC、ED相交于点F,若CD=CB,∠CDF=60°,求∠DBE的度数.
【答案】(1)① 4;②15;(2)15°.
【解析】试题分析:(1) ①先根据勾股定理求出AB,再根据角平分线的性质可证得:CD=DE,利用HL判定Rt△DCB≌Rt△DEB,所以CB=EB=6,然后根据线段和差关系计算AE的长度,
②设DC=x,则DE= x ,AD=8-x,在Rt△ADE中,利用勾股定理列方程,求出x,可得DE,然后利用三角形面积公式进行计算求△ADB的面积,
(2)根据∠CDF=60°,可得∠ADE=60°,因为DE⊥AB,所以∠DAE=90°-60°=30°,
所以∠ABC=90°-30°=60°,根据角的和差关系可求得∠DBE的度数.
试题解析:(1) ①在Rt△ABC中,AC=8,BC=6,由勾股定理可得:
AB=![]() ,
,
因为BD平分∠ABC, ∠ACB=90°,DE⊥AB,
所以DC=DE,
在Rt△DCB和Rt△DEB中,
![]() ,
,
所以Rt△DCB≌Rt△DEB,
所以EB=CB=6,
所以AE=AB-EB=10-6=4,
②设DC=x,则DE= x ,AD=8-x,
在Rt△ADE中,由勾股定理可得:
![]() ,即
,即![]() ,
,
解得x=3,即DE=3,
所以![]() .
.
(2)因为∠CDF=60°,
所以∠ADE=60°,
因为DE⊥AB,
所以∠DAE=90°-60°=30°,
所以∠ABC=90°-30°=60°,
又因为DC=BC,∠BCD=90°,
所以∠CBD=45°,
所以∠DBE=∠ABC-∠CBD=60°-45°=15°.

 阅读快车系列答案
阅读快车系列答案