题目内容
【题目】小明对函数![]() 的图象和性质进行了探究.已知当自变量
的图象和性质进行了探究.已知当自变量![]() 的值为
的值为![]() 或
或![]() 时,函数值都为
时,函数值都为![]() ;当自变量
;当自变量![]() 的值为
的值为![]() 或
或![]() 时,函数值都为
时,函数值都为![]() .探究过程如下,请补充完整.
.探究过程如下,请补充完整.
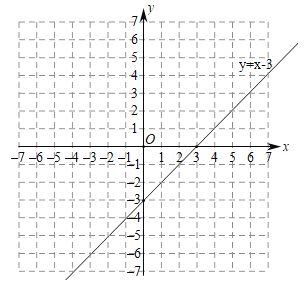
(1)这个函数的表达式为 ;
(2)在给出的平面直角坐标系中,画出这个函数的图象并写出这个函数的--条性质: ;
(3)进一步探究函数图象并解决问题:
①直线![]() 与函数
与函数![]() 有三个交点,则
有三个交点,则![]() ;
;
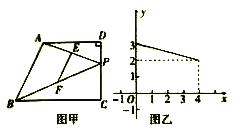
②已知函数![]() 的图象如图所示,结合你所画的函数图象,写出不等式
的图象如图所示,结合你所画的函数图象,写出不等式![]()
![]() 的解集: .
的解集: .
【答案】(1)![]() ;(2)如图所示,见解析;性质:函数的图象关于直线
;(2)如图所示,见解析;性质:函数的图象关于直线![]() 对称;或:当
对称;或:当![]() 或
或![]() 时,函数有最小值
时,函数有最小值![]() ;(3)①
;(3)①![]() ;②
;②![]() 或
或![]() .
.
【解析】
(1)将![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() 代入
代入![]() ,得到:
,得到:![]() ,
,![]() ,
,![]() ,即可求解析式为
,即可求解析式为![]() ;
;
(2)描点法画出函数图象,函数关于![]() 对称;
对称;
(3)①从图象可知:当![]() 时,
时,![]() ,
,![]() 时直线
时直线![]() 与函数
与函数![]() 有三个交点;
有三个交点;
②![]() 与
与![]() 的交点为
的交点为![]() 或
或![]() ,结合图象,
,结合图象,![]() 的解集为
的解集为![]() .
.
解:(1)将![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() 代入
代入![]() ,
,
得到: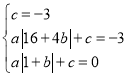 ,解得
,解得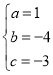
![]() ,
,
故答案为![]() .
.
(2)如图:
函数关于直线![]() 对称,
对称,
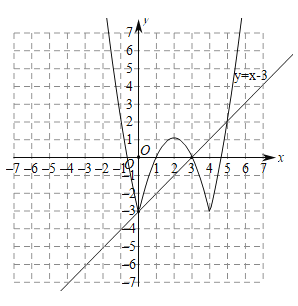
(3)①当![]() 时,
时,![]() ,
,
![]() 时直线
时直线![]() 与函数
与函数![]() 有三个交点,
有三个交点,
故答案为1;
②![]() 与
与![]() 的交点为
的交点为![]() 或
或![]() 或x=3,
或x=3,
结合图象,![]() 的解集为
的解集为![]() 或
或![]() ,
,
故答案为![]() 或
或![]() .
.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目