题目内容
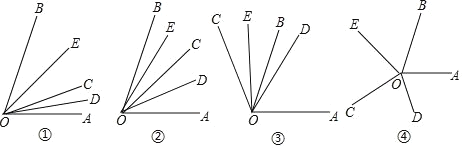
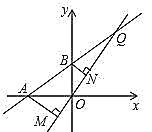
【题目】如图①所示，直线L:yax10a与x轴负半轴、y轴正半轴分别交于A、B两点.
（1）当OAOB时，试确定直线L的解析式；
（2）在（1）的条件下，如图②所示，设Q为AB延长线上一点，作直线OQ，过A、B两点分别作AMOQ于M，BNOQ于N，若AM8,BN6，求MN的长.
（3）当a取不同的值时，点B在y轴正半轴上运动，分别以OB、AB为边，点B为直角顶点在第一、二象限内作等腰直角OBF和等腰直角ABE，连接EF交y轴于P点，如图③，问：当点B在y轴正半轴上运动时，试猜想PB的长是否为定值，若是，请求出其值，若不是，说明理由.
【答案】（1）L的解析式y=x+10；（2）MN =14；（3）PB的长为定值，PB=5，见解析.
【解析】
（1）先求出直线y=ax+10a与x、y轴的交点坐标，然后由OA=OB可求出a的值，进而确定直线解析式；
（2）用AAS证明△AMO≌△ONB，由全等三角形的性质得ON=AM，OM=BN，进一步即可求出MN的值；
（3）过点E作EG⊥y轴于G点，先证明△ABO≌△EGB，得BG=AO=10，OB=EG，再证明△BFP≌△GEP，得BP=GP=
BG=5，于是问题得解.
解：（1）（1）∵直线L：y=ax+10a，
∴A（-10，0），B（0，10a），
∵直线交y轴正半轴，∴10a＞0，∴a＞0.
由OA=OB得：10a=10，∴a=1，
∴直线解析式为：y=x+10；
（2）∵AM⊥OQ，BN⊥OQ，∴∠AMO=∠BNO=90°，
∴∠AOM+∠MAO=90°，
∵∠AOM+∠BON=90°，∴∠MAO=∠NOB.
在△AMO和△OBN中，
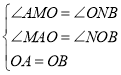
∴△AMO≌△ONB．∴ON=AM，OM=BN，
∵AM=8，BN=6，∴MN=AM+BN=14.
（3）PB的长为定值.
理由：如图，过点E作EG⊥y轴于G点，
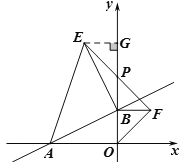
∵△AEB为等腰直角三角形，∴AB=EB，∠ABO+∠EBG=90°，
∵EG⊥BG，∴∠GEB+∠EBG=90°.
∴∠ABO=∠GEB.
在△ABO和△EGB中
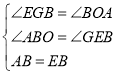
∴△ABO≌△EGB，∴BG=AO=10，OB=EG，
∵△OBF为等腰直角三角形，∴OB=BF，∴BF=EG.
在△BFP和△GEP中
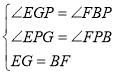
∴△BFP≌△GEP，∴BP=GP=BG=5.
即PB的长为定值.
【题目】为了增强环境保护意识，
月 
日“世界环境日”当天，若干名“环境小卫士”组成了“控制噪声污染”课题学习研究小组．该小组抽样调查了全市 
个噪声测量点在某时刻的噪声声级（单位：
），将调查的数据进行处理（设所测数据均为正整数），得频数分布表如表：
组 别 | 噪声声级分组 | 频 数 | 频 率 |
1 | 44.5--59.5 | 4 | 0.1 |
2 | 59.5--74.5 | a | 0.2 |
3 | 74.5--89.5 | 10 | 0.25 |
4 | 89.5--104.5 | b | c |
5 | 104.5--119.5 | 6 | 0.15 |
合 计 | 40 | 1.00 |
根据表中提供的信息解答下列问题：
（1）频数分布表中的 
，
，
；
（2）补全完整频数分布直方图（如图）；
（3）从这个统计中，你认为噪声污染的噪音声级分布情况怎样?
