题目内容
【题目】如图,OC是∠AOB内一条射线,OD、OE分别是∠AOC、∠BOC的平分线.
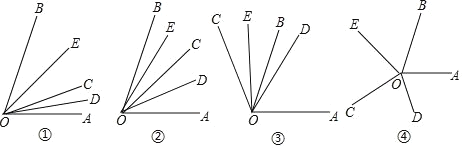
(1)如图①,当∠AOB=80°时,∠DOE=_______°;
(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠BOE、∠EOD、∠DOA三角之间有怎样的数量关系?并说明理由;
(3)当射线OC在∠AOB外如图③所示位置时,(2)中三个角:∠BOE、∠EOD、∠DOA之间数量关系是_______;
(4)当射线OC在∠AOB外如图④所示位置时,∠BOE、∠EOD、∠DOA之间数量关系是_______.
【答案】(1)40°(2)![]() (3)不成立,理由见解析.(4)∠DOE=∠BOE+∠DOA.
(3)不成立,理由见解析.(4)∠DOE=∠BOE+∠DOA.
【解析】
(1)(2)根据角平分线定义得出∠DOC=![]() ∠AOC,
∠AOC,![]() ,求出∠DOE=
,求出∠DOE=
![]()
![]() ,即可得出答案;
,即可得出答案;
(3)根据角平分线定义得出∠DOC=![]() ∠AOC,∠EOC=
∠AOC,∠EOC=![]() ∠BOC,求出∠DOE=
∠BOC,求出∠DOE=![]() ∠AOC-∠BOC)=
∠AOC-∠BOC)=![]() ∠AOB,即可得出答案;
∠AOB,即可得出答案;
(4)根据角平分线定义即可求解.
当射线OC在∠AOB的内部时,
∵OD,OE分别为∠AOC,∠BOC的角平分线,
∠DOC=![]() ∠AOC,∠EOC=
∠AOC,∠EOC=![]() ∠BOC,
∠BOC,
∴∠DOE=∠DOC+∠EOCP=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB,
∠AOB,
(1)若∠AOB=80°,则∠DOE的度数为40°
故答案为:40;
(2)![]()
(3)当射线OC在∠AOB的外部时(1)中的结论不成立.理由是:
∵OD、OE分别是∠AOC、∠BOC的角平分线,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
(4)∵OD,OE分别为∠AOC',∠BOC的角平分线,
![]() ,
,
![]() ,
,
故∠BOE、∠EOD、∠DOA之间数量关系是:
![]()
故答案为:∠DOE=∠BOE+∠DOA.

【题目】用火柴棒按下列方式搭建三角形:

(1)填表:
三角形个数 | 1 | 2 | 3 | 4 | … |
火柴棒根数 | … |
(2)当三角形的个数为![]() 时,火柴棒的根数是多少?
时,火柴棒的根数是多少?
(3)求当![]() 时,有多少根火柴棒?
时,有多少根火柴棒?
(4)当火柴棒的根数为2017时,三角形的个数是多少?
【题目】从一副52张(没有大小王)的扑克中,每次抽出1张,然后放回洗匀再抽,在实验中得到下列表中部分数据:
实验次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
出现方块的次数 | 11 | 18 | a | 40 | 49 | 63 | 68 | 80 | 91 | 100 |
出现方块的频率 | 27.5% | 22.5% | 25% | 25% | 24.5% | 26.25% | 24.3% | b | 25% | 25% |
(1)填空a= ,b= ;
(2)从上面的图表中可以估计出现方块的概率是 ;
(3)将这幅扑克中的所有方块(即从方块1到方块13,共13张)取出,将它们背面朝上重新洗牌后,从中摸出一张,若摸出的这张牌面数字为奇数,则甲方贏,若摸出的这张牌的牌面数字是偶数,则乙方赢,你认为这个游戏对双方是公平的吗说明理由.