题目内容
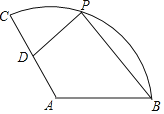
【题目】如图，在扇形CAB中，CA=4，∠CAB=120°，D为CA的中点，P为弧BC上一动点（不与C，B重合），则2PD+PB的最小值为（ ）
A. 
B. 
C. 10 D. 
【答案】D
【解析】
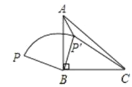
如图，作∥∠PAP′=120°，则AP′=2AB=8，连接PP′，BP′，则∠1=∠2，推出△APD∽△ABP′，得到BP′=2PD，于是得到2PD+PB=BP′+PB≥PP′，根据勾股定理得到PP′=
，求得2PD+PB≥4
，于是得到结论．
如图，作∥∠PAP′=120°，则AP′=2AB=8，连接PP′，BP′，
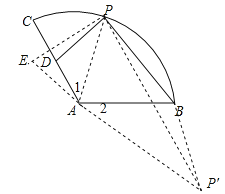
则∠1=∠2，
∵
=2，
∴△APD∽△ABP′，
∴BP′=2PD，
∴2PD+PB=BP′+PB≥PP′，
∴PP′=，
∴2PD+PB≥4，
∴2PD+PB的最小值为4，
故选D．
练习册系列答案
相关题目
