题目内容
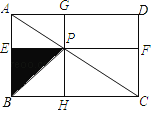
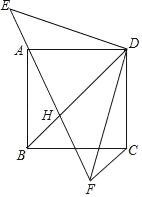
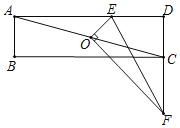
【题目】已知,O是矩形ABCD的对角线AC的中点,E是线段AD上的一点,作OF⊥OE于点O,交直线CD于点F,连结EF,若EF=2CF=2,则AE=_____.
【答案】![]() .
.
【解析】
延长EO交BC于点G,连接GF,根据矩形的性质证△AOE≌△COG,根据全等三角形的性质可证OF是EG的垂直平分线,求得FG、FC的长,用勾股定理求解即可.
如图,

延长EO交BC于点G,连接GF,
∵O是矩形ABCD的对角线AC的中点,
∴OA=OC,
∵AD∥BC,
∴∠OAE=∠OCG,∠AOE=∠COG
∴△AOE≌△COG(AAS),
∴AE=CG,OE=OG.
∵OF⊥OE,
∴OF是EG的垂直平分线,
∴FG=EF=2,
∵CF=1,∠GCF=90°,
∴CG=![]() =
=![]() ,
,
∴AE=![]() .
.
故答案为![]() .
.

练习册系列答案
相关题目