题目内容
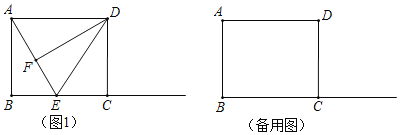
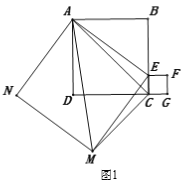
【题目】如图1,三个正方形ABCD、AEMN、CEFG,其中顶点D、C、G在同一条直线上,点E是BC边上的动点,连结AC、AM.
(1)求证:△ACM∽△ABE.
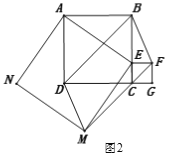
(2)如图2,连结BD、DM、MF、BF,求证:四边形BFMD是平行四边形.
(3)若正方形ABCD的面积为36,正方形CEFG的面积为4,求五边形ABFMN的面积.
【答案】(1)证明见解析;(2)证明见解析;(3)74.
【解析】
(1)根据四边形ABCD和四边形AEMN都是正方形得![]() ,∠CAB=∠MAC=45°,∠BAE=∠CAM,可证△ACM∽△ABE;
,∠CAB=∠MAC=45°,∠BAE=∠CAM,可证△ACM∽△ABE;
(2)连结AC,由△ACM∽△ABE得∠ACM=∠B=90°,易证∠MCD=∠BDC=45°,得BD∥CM,由MC=![]() BE,FC=
BE,FC=![]() CE,得MF=BD,从而可以证明四边形BFMD是平行四边形;
CE,得MF=BD,从而可以证明四边形BFMD是平行四边形;
(3)根据S五边形ABFMN=S正方形AEMN+S梯形ABFE+S三角形EFM求解即可.
(1)证明:∵四边形ABCD和四边形AEMN都是正方形,
∴![]() ,∠CAB=∠MAC=45°,
,∠CAB=∠MAC=45°,
∴∠CAB-∠CAE=∠MAC-∠CAE,
∴∠BAE=∠CAM,
∴△ACM∽△ABE.
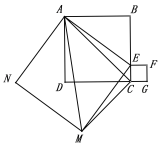
(2)证明:连结AC
因为△ACM∽△ABE,则∠ACM=∠B=90°,
因为∠ACB=∠ECF=45°,
所以∠ACM+∠ACB+∠ECF=180°,
所以点M,C,F在同一直线上,所以∠MCD=∠BDC=45°,
所以BD平行MF,
又因为MC=![]() BE,FC=
BE,FC=![]() CE,
CE,
所以MF=![]() BC=BD,
BC=BD,
所以四边形BFMD是平行四边形
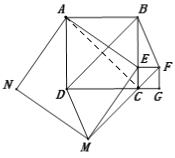
(3)S五边形ABFMN=S正方形AEMN+S梯形ABFE+S三角形EFM
=62+42+![]() (2+6)
(2+6)![]() 4+
4+![]()
![]() 2
2![]() 6
6
=74.

练习册系列答案
相关题目