题目内容
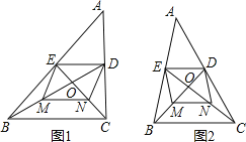
【题目】在△ABC中,BD、CE分别是边AC、AB上的中线,BD与CE交于点O.
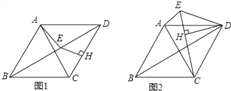
(1)如图1,若M、N分别是OB、OC的中点,求证:OB=2OD;
(2)如图2,若BD⊥CE,AB=8,BC=6,求AC的长.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)依据三角形中位线定理,即可得到DE∥BC,DE=![]() BC,再根据相似三角形的性质即可得到结论;
BC,再根据相似三角形的性质即可得到结论;
(2)依据AB=8,BC=6,点D,点E分别是AC,AB的中点,即可得出BE=4,DE=3,再根据勾股定理即可得到DE2+BC2=BE2+BC2,进而得到AC的长.
解:(1)∵BD、CE分别是边AC、AB上的中线,
∴点D,点E分别是AC,AB的中点,
∴DE是△ABC的中位线,
∴DE//BC,DE=![]() BC,
BC,
同理可证:MN//BC,MN=![]() BC,
BC,
∴四边形DEMN是平行四边形,
∴OD=OM,
∵OB=2OM,
∴OB=2OD;
(2)∵AB=8,BC=6,点D,点E分别是AC,AB的中点,
∴BE=4, DE=3,
又∵BD⊥CE,
∴DE2=DO2+EO2,BC2=BO2+CO2,
BE2=BO2+EO2,CD2=DO2+CO2,
∴DE2+BC2=BE2+CD2,
即32+62=42+CD2,
解得CD=![]() ,
,
∴AC=2CD=![]() .
.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目