题目内容
【题目】如图,已知直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,与直线
,与直线![]() 交于点
交于点![]() .点
.点![]() 从点
从点![]() 出发以每秒1个单位的速度向点
出发以每秒1个单位的速度向点![]() 运动,运动时间设为
运动,运动时间设为![]() 秒.
秒.
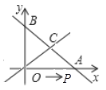
(1)求点![]() 的坐标;
的坐标;
(2)求下列情形![]() 的值;
的值;
①连结![]() ,
,![]() 把
把![]() 的面积平分;
的面积平分;
②连结![]() ,若
,若![]() 为直角三角形.
为直角三角形.
【答案】(1)点C的坐标为![]() ;(2)①t的值为2;②t的值为
;(2)①t的值为2;②t的值为![]() 或
或![]() .
.
【解析】
(1)联立两条直线的解析式求解即可;
(2)①根据三角形的面积公式可得,当BP把![]() 的面积平分时,点P处于OA的中点位置,由此即可得出t的值;
的面积平分时,点P处于OA的中点位置,由此即可得出t的值;
②先由点C的坐标可求出![]() ,再分
,再分![]() 和
和![]() 两种情况,然后利用等腰直角三角形的性质求解即可.
两种情况,然后利用等腰直角三角形的性质求解即可.
(1)由题意,联立两条直线的解析式得
解得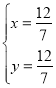
故点C的坐标为![]() ;
;
(2)①直线![]() ,令
,令![]() 得
得![]() ,解得
,解得![]()
则点A的坐标为![]() ,即
,即![]()
当点P从点O向点A运动时,t的最大值为![]()
BP将![]() 分成
分成![]() 和
和![]() 两个三角形
两个三角形
由题意得![]() ,即
,即![]()
则![]() ,即此时,点P为OA的中点
,即此时,点P为OA的中点
![]()
![]() ,符合题意
,符合题意
故t的值为2;
②由(1)点C坐标可得![]()
若![]() 为直角三角形,有以下2中情况:
为直角三角形,有以下2中情况:
当![]() 时,
时,![]() 为等腰直角三角形,且
为等腰直角三角形,且![]()
由点C坐标可知,此时![]() ,则
,则![]()
故![]() ,且
,且![]() ,符合题意
,符合题意
当![]() 时,
时,![]() 为等腰直角三角形,且
为等腰直角三角形,且![]()
由勾股定理得![]()
故![]() ,且
,且![]() ,符合题意
,符合题意
综上,t的值为![]() 或
或![]() .
.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目