题目内容
【题目】如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OAOB=OP2,我们就把∠APB叫做∠MON的智慧角.
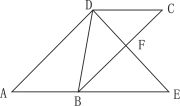
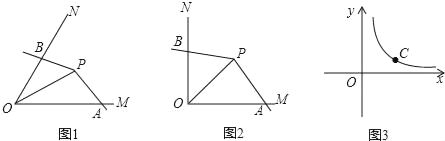
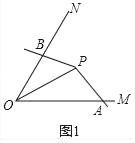
(1)如图2,已知∠MON=90°,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°.求证:∠APB是∠MON的智慧角.
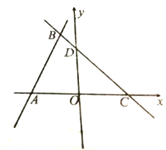
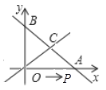
(2)如图1,已知∠MON=α(0°<α<90°),OP=2.若∠APB是∠MON的智慧角,连结AB,用含α的式子表示∠APB的度数.
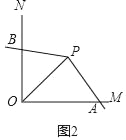
(3)如图3,C是函数![]() 图象上的一个动点,过C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
图象上的一个动点,过C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
【答案】(1)详见解析;(2)∠APB=180°﹣![]() α;(3)点P的坐标为:(
α;(3)点P的坐标为:(![]() ,
,![]() ),或(
),或(![]() ,
,![]() ).
).
【解析】
(1)只要证明△AOP∽△POB,可得![]() =
=![]() ,即可证明;
,即可证明;
(2)由∠APB是∠MON的智慧角,可得![]() =
=![]() ,即可推出△AOP∽△POB,推出∠OAP=∠OPB,推出∠APB=∠OPB+∠OPA=∠OAP+∠OPA=180°-
,即可推出△AOP∽△POB,推出∠OAP=∠OPB,推出∠APB=∠OPB+∠OPA=∠OAP+∠OPA=180°-![]() α;
α;
(3)设点C(a,b),则ab=3,过点C作CH⊥OA于H;发三种情形情况:①当点B在y轴正半轴上时;当点A在x轴的负半轴上时,如图3所示:②当点A在x轴的正半轴上时,如图4所示:③当点B在y轴的负半轴上时,如图5所示,分别求解即可.
(1)如图2中,
∵∠MON=90°,P为∠MON的平分线上一点,
∴∠AOP=∠BOP=![]() ∠MON=45°,
∠MON=45°,
∵∠AOP+∠OAP+∠APO=180°,
∴∠OAP+∠APO=135°,
∵∠APB=135°,
∴∠APO+∠OPB=135°,
∴∠OAP=∠OPB,
∴△AOP∽△POB,
∴![]() ,
,
∴OP2=OAOB,
∴∠APB是∠MON的智慧角;
(2)如图1中,
∵∠APB是∠MON的智慧角,
∴OAOB=OP2,
∴![]() ,
,
∵P为∠MON的平分线上一点,
∴∠AOP=∠BOP=![]() α,
α,
∴△AOP∽△POB,
∴∠OAP=∠OPB,
∴∠APB=∠OPB+∠OPA=∠OAP+∠OPA=180°﹣![]() α,
α,
即∠APB=180°﹣![]() α;
α;
(3)设点C(a,b),则ab=3,过点C作CH⊥OA于H;分两种情况:
①当点B在y轴正半轴上时;当点A在x轴的负半轴上时,如图3所示:
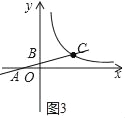
BC=2CA不可能;
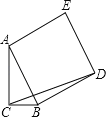
②当点A在x轴的正半轴上时,如图4所示:
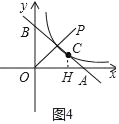
∵BC=2CA,
∴![]() ,
,
∵CH∥OB,
∴△ACH∽△ABO,
∴![]() ,
,
∴OB=3b,OA=![]() a,
a,
∴OAOB=![]() a3b=
a3b=![]() =
=![]() ,
,
∵∠APB是∠AOB的智慧角,
∴![]() ,
,
∵∠AOB=90°,OP平分∠AOB,
∴点P的坐标为:(![]() ,
,![]() );
);
③当点B在y轴的负半轴上时,如图5所示,
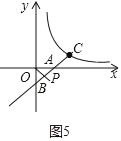
∵BC=2CA,
∴AB=CA,
在△ACH和△ABO中,
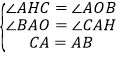 ,
,
∴△ACH≌△ABO(AAS),
∴OB=CH=b,OA=AH=![]() a,
a,
∴OAOB=![]() ab=
ab=![]() ,
,
∵∠APB是∠AOB的智慧角,
∴OP=![]() =
=![]() =
=![]() ,
,
∵∠AOB=90°,OP平分∠AOB,
∴点P的坐标为:(![]() ,
,![]() );
);
span>综上所述:点P的坐标为:(![]() ,
,![]() ),或(
),或(![]() ,
,![]() ).
).

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案【题目】某中学举办“校园好声音”朗诵大赛,根据初赛成绩,七年级和八年级各选出5名选手组成七年级代表队和八年级代表队参加学校决赛两个队各选出的5名选手的决赛成绩如图所示:
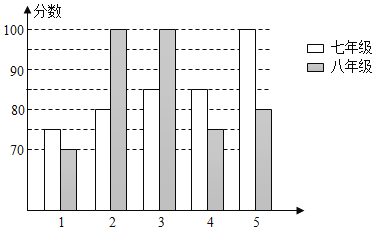
(1)根据所给信息填写表格;
平均数(分) | 中位数(分) | 众数(分) | |
七年级 | 85 | ||
八年级 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)若七年级代表队决赛成绩的方差为70,计算八年级代表队决赛成绩的方差,并判断哪个代表队的选手成绩较为稳定.