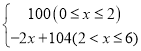题目内容
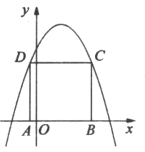
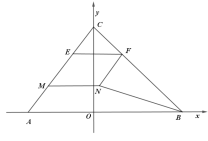
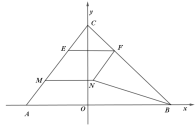
【题目】如图，在平面直角坐标系
中，
，
，
，E，M为线段AC上两个不重合的动点（点E在点M上方，且均不与端点重合），
，与BC交于点F，四边形EMNF为平行四边形，连结BN.
（1）求直线AC与直线BC的解析式；
（2）若设点F的横坐标为x，点M的纵坐标为y，当四边形EMNF为菱形时，请求y关于x的函数解析式及相应x的取值范围；
（3）请求出当
为等腰三角形时，
面积的最大值.
【答案】（1）直线AC解析式为
，直线BC解析式为
；
（2）y关于x的函数解析式为
，x的取值范围为
；
（3）
.
【解析】
（1）待定系数法求解析式即可；
（2）利用邻边相等的平行四边形是菱形的性质，用字母把邻边表示出来求解即可；
（3）首先判断等腰三角形的可能性，大胆设出F，N的坐标，列出平行四边形的面积的函数，根据二次函数的性质求最大面积.
解：(1) 设直线AC解析式为：
，将
，
代入得，
解得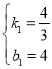
所以，直线AC解析式为.
设直线BC解析式为：
，将
，代入得，
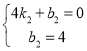解得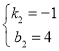
所以，直线BC解析式为.
（2）
点F的横坐标为x，且F在直线BC上，
点M的纵坐标为y，且M在直线AC上，
E、F的纵坐标相同，又E在直线AC上，
四边形EMNF为菱形，
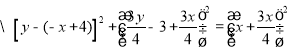
整理得：
E在M上方，即E点纵坐标大于M点纵坐标，
即
又
对两边进行开方得，
整理得：
由题知，
，即
解得
y关于x的函数解析式为，x的取值范围为.
（3）由题意当
或
时，点N在
外，不符合题意，
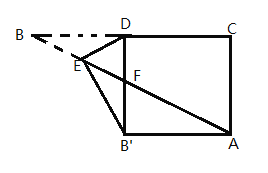
当
时，作
交EF于点D，
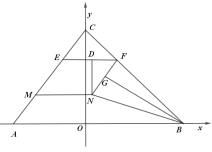
设
，
，
易得
，
，
，
，
设FN中点为点G，又，
，
∵在△BNF中，
，
，
又
，
，
，
，
解得
，
由题意
，
当
时，
的面积有最大值，
此时.
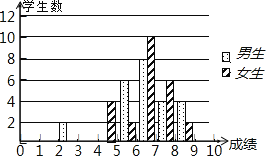
阅读快车系列答案
【题目】为了迎接体育中考，初三7班的体育老师对全班48名学生进行了一次体能模拟测试，得分均为整数，满分10分，成绩达到6分以上（包括6分）为合格，成绩达到9分以上（包括9分）为优秀，这次模拟测试中男、女生全部成绩分布的条形统计图如下
（1）请补充完成下面的成绩统计分析表：
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
男生 | 6.9 | 2.4 | ______ | 91.7% | 16.7% |
女生 | ______ | 1.3 | ______ | 83.3% | 8.3% |
（2）男生说他们的合格率、优秀率均高于女生，所以他们的成绩好于女生，但女生不同意男生的说法，认为女生的成绩要好于男生，请给出两条支持女生观点的理由；
（3）体育老师说，咱班的合格率基本达标，但优秀率太低，我们必须加强体育锻炼，两周后的目标是：全班优秀率达到50%．如果女生新增优秀人数恰好是男生新增优秀人数的两倍，那么男、女生分别新增多少优秀人数才能达到老师的目标？
