题目内容
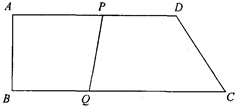28、如图，在四边形ABCD中，AD∥BC，∠B=90°，AD=18cm，BC=21cm，动点P从A开始沿AD边向D以1cm/秒的速度运动，动点Q从C点开始沿CB边以2cm/秒的速度运动，P、Q分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动的时间为t秒，t为何值时四边形PQCD为等腰梯形？分析：要使四边形PQCD为等腰梯形，由于AD∥BC，那么只需在移动的过程中满足PQ=CD即可．
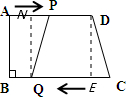
解答：解：如图所示．过点D、Q分别作DE⊥BC于E，QN⊥AD于N．
∵∠A=∠B=∠BED=90°，∴ABED为矩形，
∴AD=BE，
∵
在直角梯形ABCD中，
AD∥BC，∠B=90°，AD=18cm，BC=21cm，
∴CE=BC-BE=BC-AD=21-18=3cm．
∵四边形PQCD为等腰梯形，
∴PQ=DC，EC=NP=3，
Q点走过的路程2t=18-t+2×3，
解之得，t=8，
故t=8时四边形PQCD为等腰梯形．
∵∠A=∠B=∠BED=90°，∴ABED为矩形，
∴AD=BE，
∵
在直角梯形ABCD中，AD∥BC，∠B=90°，AD=18cm，BC=21cm，
∴CE=BC-BE=BC-AD=21-18=3cm．
∵四边形PQCD为等腰梯形，
∴PQ=DC，EC=NP=3，
Q点走过的路程2t=18-t+2×3，
解之得，t=8，
故t=8时四边形PQCD为等腰梯形．
点评：本题考查了等腰梯形的性质，要求能够解决一些简单的运动问题，熟练掌握矩形以及等腰梯形的性质及判定．
练习册系列答案
相关题目
（2013•赤峰）如图，在Rt△ABC中，∠B=90°，AC=60cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，EF．
已知：如图，在四边形ABC中，AD=BC，AB=CD．
如图，在Rt△ABC中，∠BAC=90°，将△ABC沿线段BC向右平移得到△DEF，使CE=AE，连结AD、AE、CD，则下列结论：①AD∥BE且AD=BE；②∠ABC=∠DEF；③ED⊥AC；④四边形AECD为菱形，其中正确的共有（ ）
已知：如图，在四边形ABC中，AD=BC，AB=CD．