Question

【题目】如图，在平面直角坐标系中，四边形OABC是正方形，点A的坐标是（2，1），则点C的坐标是_____．

Answer 1

【答案】（﹣1，2）

【解析】

如图，过点C作CD⊥x轴，过点A作AE⊥x轴，由“AAS”可证△AOE≌△OCD，可得DO=AE=1，CD=OE=2，即可求解．

解：如图，过点C作CD⊥x轴，过点A作AE⊥x轴，

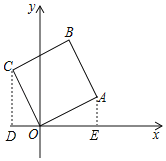
∵点A的坐标是（2，1），

∴AE＝1，OE＝2，

∵四边形OABC是正方形，

∴AO＝CO，∠AOC＝90°，

∴∠AOE+∠COD＝90°，且∠AOE+∠OAE＝90°，

∴∠COD＝∠OAE，且AO＝CO，∠AEO＝∠CDO＝90°，

∴△AOE≌△OCD（AAS）

∴DO＝AE＝1，CD＝OE＝2，

∴点C坐标为（﹣1，2）.

故答案为：（﹣1，2）