Question

【题目】在平面直角坐标系中，点A坐标是（0，a），点B坐标是（b，0），且a、b满足a2﹣12a+36+＝0

（1）求A、B两点的坐标；

（2）如图1，点C为x轴负半轴一动点，OC＜OB，BD⊥AC于D交y轴于点E，求证：DO平分∠CDB；

（3）如图2，点F为AB中点，点G为x轴正半轴点B右侧一动点，过点F作FG的垂线FH，交y轴的负半轴于点H，那么当点G的位置不断变化时，S△AFH﹣S△FBG的值是否发生变化？若变化，请说明理由，若不变化，请求出相应结果．

Answer 1

【答案】（1）点A（0，6），点B（6，0）（2）见解析;（3）S△AFH﹣S△FEG的值不发生变化，理由见解析.

【解析】

（1）由非负性可求a，b的值，即可求A、B两点的坐标；
（2）过点O作OM⊥BD于M，ON⊥AC于N，根据全等三角形的判定和性质解答即可；
（3）由于点F是等腰直角三角形AOB的斜边的中点，所以连接OF，得出OF=BF．∠BFO=∠GFH，进而得出∠OFH=∠BFG，利用等腰直角三角形和全等三角形的判定和性质以及三角形面积公式解答即可．

解：（1）∵a2﹣12a+36+＝0

∴（a﹣6）2+＝0，

∴a＝b＝6，

∴点A（0，6），点B（6，0）

（2）过点O作OM⊥BD于M，ON⊥AC于N，

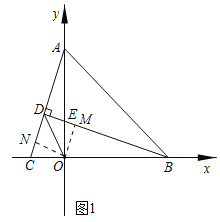
∵x轴⊥y轴

∴∠AOC＝∠BOE＝90°

∴∠ACO+∠CAO＝90°

∵BD⊥AC

∴∠BCD+∠CBE＝90°

∴∠CAO＝∠CBE，

∵点A，B的坐标分别为（0，6），（6，0）

∴OA＝OB＝6，

在△AOC和△BOE中,

∴△AOC≌△BOE（ASA）

∴OE＝OC，S△AOC＝S△BOE，AC＝BE，

∴ACON＝BCOM

∴OM＝ON，且OM⊥BD，ON⊥AC，

∴点O一定在∠CDB的角平分线上

即OD平分∠CDB；

（3）S△AFH﹣S△FEG的值不发生变化，

理由如下：

如图2，连接OF，

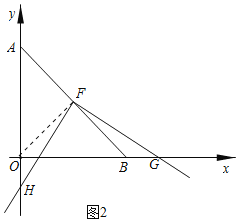
∵△AOB是等腰直角三角形且点F为AB的中点

∴OF⊥AB，OF＝FB，OF平分∠AOB

∴∠OFB＝∠OFH+∠HFB＝90°

又∵FG⊥FH

∴∠HFG＝∠BFG+∠HFB＝90°

∴∠OFH＝∠BFG

∵∠FOB＝∠AOB＝45°，

∴∠FOH＝∠FOB+∠HOB＝45°+90°＝135°

又∵∠FBG＝180°﹣∠ABO＝180°﹣45°＝135°

∴∠FOH＝∠FBG

在△FOH和△FBG中,

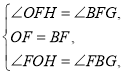
∴△FOH≌△FBG（ASA）

∴S△AOC＝S△BOE

∴S△AFH﹣S△FBG

＝S△AFH﹣S△FOH

＝S△FOA＝××6×6＝9．