题目内容
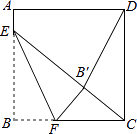
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.

(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
【答案】(1)证明见解析(2)40°
【解析】(1)证明:∵四边形ABCD是菱形,∴AB=CD,AB∥CD。
又∵BE=AB,∴BE=CD,BE∥CD。∴四边形BECD是平行四边形。
∴BD=EC。
(2)解:∵四边形BECD是平行四边形,∴BD∥CE,∴∠ABO=∠E=50°。
又∵四边形ABCD是菱形,∴AC丄BD。∴∠BAO=90°﹣∠ABO=40°
(1)根据菱形的对边平行且相等可得AB=CD,AB∥CD,然后证明得到BE=CD,BE∥CD,从而证明四边形BECD是平行四边形,再根据平行四边形的对边相等即可得证。
(2)根据两直线平行,同位角相等求出∠ABO的度数,再根据菱形的对角线互相垂直可得AC⊥BD,然后根据直角三角形两锐角互余计算即可得解。

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目