题目内容
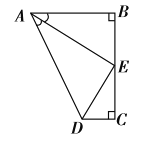
【题目】如图1,在![]() 和
和![]() 中
中![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() 绕点
绕点![]() 自由旋转.
自由旋转.

(1)当![]() 在
在![]() 边上时,
边上时,
①线段![]() 和线段
和线段![]() 的关系是____________________;
的关系是____________________;
②若![]() ,则
,则![]() 的度数为____________;
的度数为____________;
(2)如图2,点![]() 不在
不在![]() 边上,
边上,![]() ,
,![]() 相交于点
相交于点![]() ,(l)问中的线段
,(l)问中的线段![]() 和线段
和线段![]() 的关系是否仍然成立?并说明理由.
的关系是否仍然成立?并说明理由.
【答案】(1)①BD=CE,BD⊥CE,②67.5°;(2)(1)问中的线段BD和线段CE的关系仍然成立
【解析】
(1)①延长BD交CE于H,证明△ABD≌△ACE,根据全等三角形的性质得到BD=CE,∠ABD=∠ACE,求出∠CHD=90°,得到BD⊥CE,得到答案;
②根据等腰三角形的性质得到∠ABC=∠ACB=45°,根据等腰三角形的性质、三角形的外角性质计算即可;
(2)仿照(1)①的作法证明即可.
解:(1)①延长BD交CE于H,
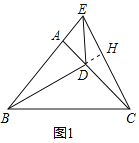
在△ABD和△ACE中,
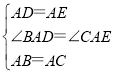
∴△ABD≌△ACE(SAS)
∴BD=CE,∠ABD=∠ACE,
∵∠ABD+∠ADB=90°,∠ADB=∠CDH,
∴∠DCH+∠CDH=90°,即∠CHD=90°,
∴BD⊥CE,
故答案为:BD=CE,BD⊥CE;
②BC=AD+AB=AE+AB=BE,
∴∠BEC=∠BCE,
∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∴∠BEC=∠BCE=67.5°,
∵BE=BC,BH⊥CE,
∴∠CBH=∠EBH=∠ACE,
∴∠ADB=∠DBC+∠DCB=∠ACE+∠DCB=67.5°,
故答案为:67.5°;
(2)(1)问中的线段BD和线段CE的关系仍然成立,
∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,即∠BAD=∠CAE
理由如下:在△ABD和△ACE中,
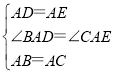
∴△ABD≌△ACE(SAS)
∴BD=CE,∠ABD=∠ACE,
∵∠ABD+∠ANB=90°,∠ANB=∠FNC,
∴∠ACF+∠DNC=90°,即∠CFN=90°,
∴BD⊥CE,
综上所述,BD=CE,BD⊥CE.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案