题目内容
【题目】如图,在矩形纸片![]() 中,
中,![]() ,折叠纸片,使点
,折叠纸片,使点![]() 刚好落在线段
刚好落在线段![]() 上,且折痕分别于
上,且折痕分别于![]() 相交,设折叠后点
相交,设折叠后点![]() 的对应点分别为点
的对应点分别为点![]() ,折痕分别于
,折痕分别于![]() 相交于点
相交于点![]() ,则线段
,则线段![]() 的取值范围是__________.
的取值范围是__________.

【答案】![]()
【解析】
由四边形ABCD是矩形,根据折叠的性质,易证得△EFG是等腰三角形,即可得GF=EC,又由GF∥EC,即可得四边形CEGF为平行四边形,根据邻边相等的平行四边形是菱形,即可得四边形BGEF为菱形,如图2,当G与A重合时,CE取最大值,由折叠的性质得CD=DG,∠CDE=∠GDE=45°,推出四边形CEGD是矩形,根据矩形的性质即可得到CE=CD=AB=3;如图1,当F与D重合时,CE取最小值,由折叠的性质得AE=CE,根据勾股定理即可得到结论.
证明:∵四边形ABCD是矩形,
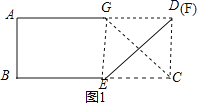
∴AD∥BC,
∴∠GFE=∠FEC,
∵图形翻折后点G与点C重合,EF为折线,
∴∠GEF=∠FEC,
∴∠GFE=∠FEG,
∴GF=GE,
∵图形翻折后BC与GE完全重合,
∴BE=EC,

∴GF=EC,
∴四边形CEGF为平行四边形,
∴四边形CEGF为菱形;
∴CE=CD=AB=3;
如图2,当G与A重合时,CE取最大值,
由折叠的性质得AE=CE,
∵∠B=90°,
∴AE2=AB2+BE2,即CE2=32+(9-CE)2,
∴CE=5,
∴线段CE的取值范围3≤CE≤5.
故答案为:3≤CE≤5.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目






