题目内容
【题目】如图,在直角△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
(1)求证:MD=ME;
(2)填空:连接OE,OD,当∠A的度数为 时,四边形ODME是菱形.
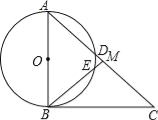
【答案】(1)证明过程见解析;(2)60°.
【解析】
试题分析:(1)、利用直角三角形斜边上的中线性质得MA=MB,则∠A=∠MBA,再利用圆内接四边形的性质证明∠MDE=∠MED,于是得到MD=ME;(2)、先证明△OAD和△OBE为等边三角形,再证明四边形DOEM为平行四边形,然后加上OD=OE可判断四边形ODME是菱形.
试题解析:(1)、在Rt△ABC中,点M是AC的中点, ∴MA=MB, ∴∠A=∠MBA;
∵四边形ABED是圆内接四边形, ∴∠ADE+∠ABE=180°, 而∠ADE+∠MDE=180°,
∴∠MDE=∠MBA; 同理可得∠MED=∠A, ∴∠MDE=∠MED, ∴MD=ME;
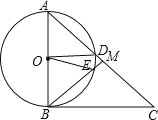
(2)、当∠A=60°时, 则∠ABM=60°, ∴△OAD和△OBE为等边三角形, ∴∠BOE=60°,
∴∠BOE=∠A, ∴OE∥AC, 同理可得OD∥BM, ∴四边形DOEM为平行四边形,
而OD=OE, ∴四边形ODME是菱形.

练习册系列答案
相关题目