题目内容
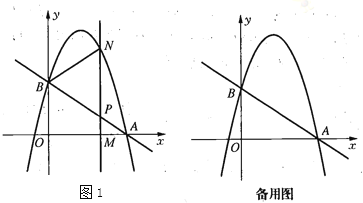
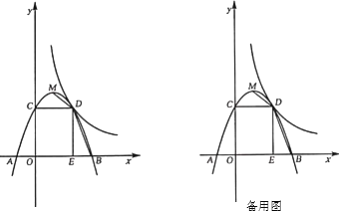
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C.
(1)求抛物线y=ax2+2x+c的解析式:;
(2)点D为抛物线上对称轴右侧、x轴上方一点,DE⊥x轴于点E,DF∥AC交抛物线对称轴于点F,求DE+DF的最大值;
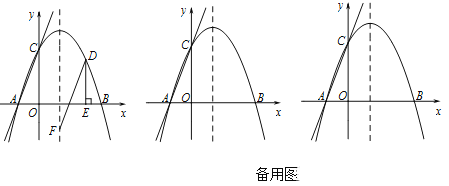
(3)①在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
②点Q在抛物线对称轴上,其纵坐标为t,请直接写出△ACQ为锐角三角形时t的取值范围.
【答案】(1)y=﹣x2+2x+3;(2)DE+DF有最大值为![]() ;(3)①存在,P的坐标为(
;(3)①存在,P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );②
);②![]() <t<
<t<![]() .
.
【解析】
(1)设抛物线解析式为y=a(x+1)(x﹣3),根据系数的关系,即可解答
(2)先求出当x=0时,C的坐标,设直线AC的解析式为y=px+q,把A,C的坐标代入即可求出AC的解析式,过D作DG垂直抛物线对称轴于点G,设D(x,﹣x2+2x+3),得出DE+DF=﹣x2+2x+3+![]() (x-1)=﹣x2+(2+
(x-1)=﹣x2+(2+![]() )x+3-
)x+3-![]() ,即可解答
,即可解答
(3)①过点C作AC的垂线交抛物线于另一点P1,求出直线PC的解析式,再结合抛物线的解析式可求出P1,过点A作AC的垂线交抛物线于另一点P2,再利用A的坐标求出P2,即可解答
②观察函数图象与△ACQ为锐角三角形时的情况,即可解答
解:(1)设抛物线解析式为y=a(x+1)(x﹣3),即y=ax2﹣2ax﹣3a,
∴﹣2a=2,解得a=﹣1,
∴抛物线解析式为y=﹣x2+2x+3;
(2)当x=0时,y=﹣x2+2x+3=3,则C(0,3),设直线AC的解析式为y=px+q,把A(﹣1,0),C(0,3)代入得![]() ,解得
,解得![]() ,∴直线AC的解析式为y=3x+3,如答图1,过D作DG垂直抛物线对称轴于点G,设D(x,﹣x2+2x+3),
,∴直线AC的解析式为y=3x+3,如答图1,过D作DG垂直抛物线对称轴于点G,设D(x,﹣x2+2x+3),
∵DF∥AC,
∴∠DFG=∠ACO,易知抛物线对称轴为x=1,
∴DG=x-1,DF=![]() (x-1),
(x-1),
∴DE+DF=﹣x2+2x+3+![]() (x-1)=﹣x2+(2+
(x-1)=﹣x2+(2+![]() )x+3-
)x+3-![]() ,
,
∴当x=![]() ,DE+DF有最大值为
,DE+DF有最大值为![]() ;
;
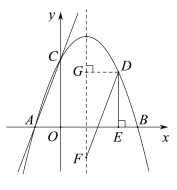
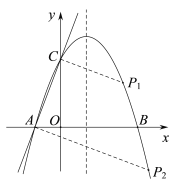
答图1 答图2
(3)①存在;如答图2,过点C作AC的垂线交抛物线于另一点P1,
∵直线AC的解析式为y=3x+3,
∴直线PC的解析式可设为y=![]() x+m,把C(0,3)代入得m=3,
x+m,把C(0,3)代入得m=3,
∴直线P1C的解析式为y=![]() x+3,解方程组
x+3,解方程组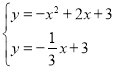 ,解得
,解得![]() 或
或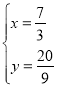 ,则此时P1点坐标为(
,则此时P1点坐标为(![]() ,
,![]() );过点A作AC的垂线交抛物线于另一点P2,直线AP2的解析式可设为y=
);过点A作AC的垂线交抛物线于另一点P2,直线AP2的解析式可设为y=![]() x+n,把A(﹣1,0)代入得n=
x+n,把A(﹣1,0)代入得n=![]() ,
,
∴直线PC的解析式为y=![]() ,解方程组
,解方程组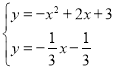 ,解得
,解得![]() 或
或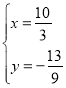 ,则此时P2点坐标为(
,则此时P2点坐标为(![]() ,
,![]() ),综上所述,符合条件的点P的坐标为(
),综上所述,符合条件的点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
②![]() <t<
<t<![]() .
.