题目内容
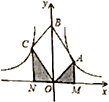
【题目】如图1,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 抛物线
抛物线![]() 经过点
经过点![]() 、
、![]() .
.
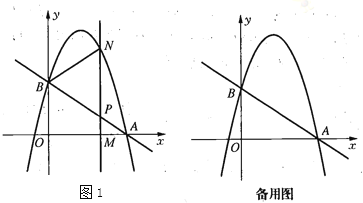
(1)求点![]() 的坐标和抛物线的解析式.
的坐标和抛物线的解析式.
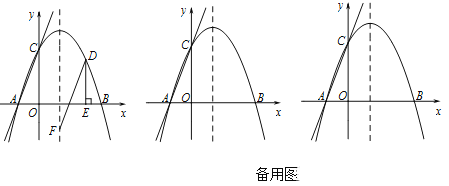
(2)![]() 为
为![]() 轴上一个动点,过点
轴上一个动点,过点![]() 垂直于
垂直于![]() 轴的直线与直线
轴的直线与直线![]() 和抛物线分别交于点
和抛物线分别交于点![]() 、
、![]() .
.
①点![]() 在线段
在线段![]() 上运动,若以
上运动,若以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标;
的坐标;
②点![]() 在
在![]() 轴上自由运动,若三个点
轴上自由运动,若三个点![]() 、
、![]() 、
、![]() 中恰有一点是其他两点所连线段的中点(三点重合除外),则称
中恰有一点是其他两点所连线段的中点(三点重合除外),则称![]() 、
、![]() 、
、![]() 三点为“共谐点”.请直接写出使得
三点为“共谐点”.请直接写出使得![]() 、
、![]() 、
、![]() 三点成为“共谐点”的
三点成为“共谐点”的![]() 的值.
的值.
【答案】(1)![]() ;抛物线的解析式为
;抛物线的解析式为![]() ;
;
(2)①点![]() 的坐标为
的坐标为![]() 或
或![]() ;②
;②![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用待定系数法即可解决问题;
(2)②先根据题意确定N点坐标,再根据(1)所得直线AB的解析式,确定OA,OB的长度,若使![]() 和
和![]() 相似,则必须
相似,则必须![]() 或
或![]() ,然后分类讨论即可;
,然后分类讨论即可;
②根据题意直接写成m的取值即可.
解:(1)∵直线![]() 与
与![]() 轴交于点
轴交于点![]() ,∴
,∴![]() ,解得
,解得![]() ,∴
,∴![]() .
.
∵抛物线![]() 经过点
经过点![]() ,∴
,∴![]() ,
,
∴![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() .
.
(2)∵![]() 轴,
轴,![]() ,
,![]() ,∴
,∴![]() .
.
①由(1)知直线![]() 的解析式为
的解析式为![]() ,
,![]() ,
,![]() .
.
在![]() 和
和![]() 中,∵
中,∵![]() ,
,![]() ,∴若使
,∴若使![]() 和
和![]() 相似,则必须
相似,则必须![]() 或
或![]() ,分两种情况讨论如下:
,分两种情况讨论如下:
(Ⅰ)当![]() 时,过点
时,过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() ,即
,即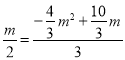 ,解得
,解得![]() (舍去)或
(舍去)或![]() ,
,
∴![]() .
.
(Ⅱ)当![]() 时,
时,![]() ,∴点
,∴点![]() 的纵坐标为2,∴
的纵坐标为2,∴![]() ,解得
,解得![]() (舍去)或
(舍去)或![]() ,∴
,∴![]() .
.
综上,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
②![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目