Question

【题目】如图，Rt△ABC的三个顶点的坐标分别为A(-3，2)、B(0，4)、C(0，2).

⑴将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C．平移△ABC，若A对应点A2的坐标为(0，-4)，画出平移后对应的△A2B2C2；

⑵若将△A1B1C绕某一点旋转得到△A2B2C2，请直接写出旋转中心的坐标为 ．

⑶在x轴上找一点P，使得直线CP将△ABC的面积分为1：2，直接写出P点的坐标为 .

Answer 1

【答案】（1）见解析；（2） (，-1)；（3）(6，0)或(，0)

【解析】

（1）根据关于中心对称的性质和网格特点画出A、B点的对应点A1，B1，从而得到△A1B1C；根据A点和A2点的坐标，确定平移的方向和平移的距离，然后根据点平移的规律写出B2、C2的坐标；

（2）连接CC2，旋转中心为CC2的中点；

（3）在AC上取点F（-2，0）、G（-1，0），分别过点F、G作x轴垂线交AB于E、D，求出直线CE、CD的解析式，即可得到P点坐标．

解：(1)如图，

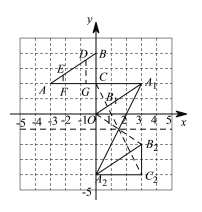
(2)连接CC2，旋转中心为CC2的中点，由（1）中可知C(0，2)， C2 (3，-4)

因此旋转中心为(，-1)．

(3) 在AC上取点F（-2，0）、G（-1，0），分别过点F、G作x轴垂线交AB于E、D，

则直线CE、CD即为直线CP的位置，

∴EF=BC，DG=BC，

∴E（-2，）、G（-1，），

然后求出直线CE解析式为，时，，

∴P坐标为(6，0)，

求出直线CD解析式为，时，，

∴P坐标为(，0)，

故答案为：(6，0)或(，0)．