题目内容
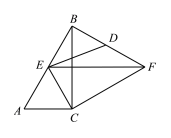
【题目】已知:在![]() 和
和![]() 中,
中,![]() ,
,![]() ,将
,将![]() 如图放置,使得
如图放置,使得![]() 的两条边分别经过点
的两条边分别经过点![]() 和点
和点![]() .
.
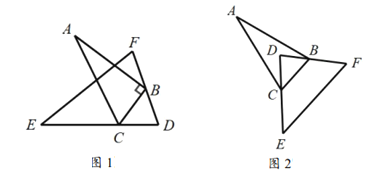
(1)当将![]() 如图1摆放时,
如图1摆放时,![]() ______
______![]() .
.
(2)当将![]() 如图2摆放时,试问:
如图2摆放时,试问:![]() 等于多少度?请说明理由.
等于多少度?请说明理由.
(3)如图2,是否存在将![]() 摆放到某个位置时,使得
摆放到某个位置时,使得![]() ,
,![]() 分别平分
分别平分![]() 和
和![]() ?如果存在,请画出图形或说明理由.如果不存在,请改变题目中的一个已知条件,使之存在.
?如果存在,请画出图形或说明理由.如果不存在,请改变题目中的一个已知条件,使之存在.
【答案】(1)116;(2)316;(3)不存在,理由详见解析.
【解析】
(1)由三角形内角和定理得:∠D=180°-(∠E+∠F)=80°,∠DBC+∠DCB=180°-∠D=100°,∠ABC+∠ACB=180°-∠A=144°,求出∠ABF+∠ACE=180°-(∠ABC+∠DBC)+180°-(∠ACB+∠DCB),即可得出结果;
(2)由三角形内角和定理得出∠ABC+∠ACB=180°-∠A=144°,∠D=80°,∠BCD+∠CBD=180°-∠D=100°,得出∠ABD+∠ACD=(∠ABC+∠ACB)-(∠BCD+∠CBD)=44°,再由平角的性质即可得出结果;
(3)假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.则∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,所以不存在.如果存在,根据两内角平分线模型,可知∠D=90°+ ![]() ∠A,题中∠D=80°,∠A=36°,只要∠E+∠F=100°改成∠E+∠F=72°即可.
∠A,题中∠D=80°,∠A=36°,只要∠E+∠F=100°改成∠E+∠F=72°即可.
解:(1)由三角形内角和定理得:∠D=180°-(∠E+∠F)=180°-100°=80°,
∴∠DBC+∠DCB=180°-∠D=100°,
∵∠ABC+∠ACB=180°-∠A=144°,
∴∠ABF+∠ACE=180°-(∠ABC+∠DBC)+180°-(∠ACB+∠DCB)=360°-100°-144°=116°;
故答案为:116;
(2)∠ABF+∠ACE=316°;理由如下;在△ABC中,∠A=36°,
∴∠ABC+∠ACB=180°-∠A=144°,
在△DEF中,∠E+∠F=100°,
∴∠D=180°-100°=80°,
∴∠BCD+∠CBD=180°-∠D=100°,
∴∠ABD+∠ACD=(∠ABC+∠ACB)-(∠BCD+∠CBD)=144°-100°=44°,
∴∠ABF+∠ACE=180°-∠ABD+180°-∠ACD=360°-(∠ABD+∠ACD)=360°-44°=316°;
(3)不存在.假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.
则∠CBD+∠BCD=∠ABD+∠ACD=100°,
那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,
∴不存在;
如果存在,根据两内角平分线模型,可知∠D=90°+![]() ∠A,题中∠D=80°,∠A=36°,
∠A,题中∠D=80°,∠A=36°,
∴只要∠E+∠F=100°改成∠E+∠F=72°.