题目内容
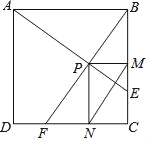
【题目】如图,已知一条直线过点![]() ,且与抛物线
,且与抛物线![]() 交于A、B两点,其中点A的横坐标是-2.
交于A、B两点,其中点A的横坐标是-2.
⑴求这条直线的函数关系式及点B的坐标 ;
⑵在![]() 轴上是否存在点C,使得ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在点C,使得ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
⑶.过线段AB上一点P,作PM∥![]() 轴,交抛物线于点M,点M在第一象限;点
轴,交抛物线于点M,点M在第一象限;点![]() ,当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
,当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?

【答案】(1)点B的坐标为(8,16);(2)点C的坐标为(![]() ,0),(0,0),(6,0),(32,0);(3)当M的横坐标为6时,MN+3PM的长度的最大值是18.
,0),(0,0),(6,0),(32,0);(3)当M的横坐标为6时,MN+3PM的长度的最大值是18.
【解析】试题分析:(1)、根据点A在二次函数上求出点A的坐标,然后利用待定系数法求出一次函数的解析式,根据一次函数和二次函数的交点坐标求出求出点B的坐标;(2)、根据点A和点B的坐标求出![]() 的值,设点C的坐标为(m,0),然后分别求出
的值,设点C的坐标为(m,0),然后分别求出![]() 和
和![]() 的值,然后根据勾股定理分三种情况进行讨论,分别求出m的值,得出点C的坐标;(3)、设点M的坐标为:(a,
的值,然后根据勾股定理分三种情况进行讨论,分别求出m的值,得出点C的坐标;(3)、设点M的坐标为:(a, ![]() ),MP与y轴交于点Q,根据Rt△MQN的勾股定理求出MN的长度,根据点P和点M的纵坐标相等得出点P的横坐标为
),MP与y轴交于点Q,根据Rt△MQN的勾股定理求出MN的长度,根据点P和点M的纵坐标相等得出点P的横坐标为![]() ,从而得出MN+3MP关于a的函数解析式,然后利用二次函数的性质得出最大值.
,从而得出MN+3MP关于a的函数解析式,然后利用二次函数的性质得出最大值.
试题解析:(1)、∵点A是直线与抛物线的交点,且横坐标为﹣2,
∴y=![]() ×(﹣2)2=1,A点的坐标为(﹣2,1),
×(﹣2)2=1,A点的坐标为(﹣2,1),
设直线的函数关系式为y=kx+b,
将(0,4),(﹣2,1)代入得: ![]() ,解得:
,解得: 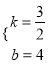 ,
,
∴直线y=![]() x+4, ∵直线与抛物线相交, ∴
x+4, ∵直线与抛物线相交, ∴![]() x+4=
x+4=![]() x2,解得:x=﹣2或x=8,
x2,解得:x=﹣2或x=8,
当x=8时,y=16, ∴点B的坐标为(8,16);
(2)、如图1,连接AC,BC, ∵由A(﹣2,1),B(8,16)可求得AB2=325.
设点C(m,0),同理可得AC2=(m+2)2+12=m2+4m+5, BC2=(m﹣8)2+162=m2﹣16m+320,
①若∠BAC=90°,则AB2+AC2=BC2,即325+m2+4m+5=m2﹣16m+320,解得:m=﹣![]() ;
;
②若∠ACB=90°,则AB2=AC2+BC2,即325=m2+4m+5+m2﹣16m+320, 解得:m=0或m=6;
③若∠ABC=90°,则AB2+BC2=AC2,即m2+4m+5=m2﹣16m+320+325, 解得:m=32;
∴点C的坐标为(﹣![]() ,0),(0,0),(6,0),(32,0)
,0),(0,0),(6,0),(32,0)
(3)设M(a, ![]() ),设MP与y轴交于点Q,
),设MP与y轴交于点Q,
在Rt△MQN中,由勾股定理得MN=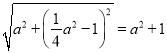 ,
,
又∵点P与点M纵坐标相同, ∴![]() +4=
+4=![]() , ∴x=
, ∴x=![]() , ∴点P的横坐标为
, ∴点P的横坐标为![]() ,
,
∴MP=a﹣![]() , ∴MN+3PM=
, ∴MN+3PM=![]() +1+3(a﹣
+1+3(a﹣![]() )=﹣
)=﹣![]() +3a+9,
+3a+9,

∴当a=﹣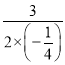 =6, 又∵﹣2≤6≤8, ∴取到最大值18,
=6, 又∵﹣2≤6≤8, ∴取到最大值18,
∴当M的横坐标为6时,MN+3PM的长度的最大值是18.

 名校课堂系列答案
名校课堂系列答案【题目】为了丰富学生校园生活,满足学生的多元文化需求,促进学生身心健康和谐发展,学校开展了丰富多彩的社团活动.我区某中学开展的社团活动有:A.尤克里里、B.街舞、C.羽毛球、D.口琴、E.沙画.学生管理中心为了了解全校800名学生的社团需求,开展了一次调查研究,请将下面的调查过程补全.
抽样调查:学生管理中心计划选取40名学生进行问卷调查,下面的抽样方法中, 合理的是 (填序号);
①从七、八、九三个年级中随机抽取40名女生进行问卷调查;
②从七、八、九三个年级中随机抽取男、女生共40名进行问卷调查.
收集数据:抽样方法确定后,学生管理中心收集到如下数据(社团项目的编号,用字母代号表示)
B,E,B,A,E,C,C,C,B,B
A,C,E,D,B,A,B,E,C,A
D,D,B,B,C,C,A,A,E,B
C,B,D,C,A,C,C,A,C,E
整理、描述数据:划记、整理、描述样本数据、绘制统计图如下,请补全统计表和统计图.
选择各社团项目的人数统计表
社团项目 | 划记 | 人数 |
A尤克里里 | 正 | 8 |
B街舞 | ||
C羽毛球 | 正正丅 | 12 |
D口琴 | ||
E沙画 | 正一 | 6 |
合计 | 40 | 40 |

分析数据、推断结论:
(1)在扇形统计图中,“B街舞”所在的扇形的圆心角等于 度;
(2)根据学生管理中心获得的样本数据估计全校大约有多少名同学选择羽毛球这个社团?