题目内容
【题目】如图1,Rt△ABC和Rt△DBE中,∠ABC=∠EBD=90°,AB=BC,DB=EB.显然可得结论AD=EC,AD⊥EC.
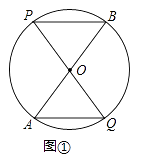
(1)阅读:当Rt△DBE绕点B逆时针旋转到图2的位置时,连接AD,CE.求证:AD=EC,AD⊥EC.
下面给出了小亮的证明过程,请你把小亮的证明过程填写完整:
∵∠ABC=∠EBD,∴∠ABC-∠ABE=∠EBD-∠ABE,即∠EBC=∠DBA.在△EBC和△DBA中,
BC=BA,∠______=∠______,BE=BD,
∴△EBC≌△DBA,∴CE=AD,∠ECB=∠______.
∵∠ECB+∠ACE+∠CAB=90°,∴∠DAB+∠ACE+∠CAB=90°,∴∠______=90°,∴AD⊥EC.
(2)类比:当Rt△DBE绕点B逆时针旋转90°得到图3时,连接AD,CE.问(1)中线段AD,EC间的数量关系和位置关系还成立吗?若成立,请给出证明;若不成立,请说明理由;
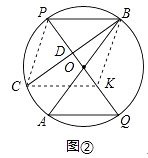
(3)拓展:当Rt△DBE绕点B逆时针旋转到图4时,连接AD,CE.请说明AD,EC间的数量关系和位置关系.

【答案】 (1)EBC DBA DAB AKC
(2)成立,理由见解析;(3)AD=EC,AD⊥EC.
【解析】(1)根据证明过程直接填空即可;
(2)先证△ADB与△CBE全等,得出CE=AD,和∠ECB=∠DAB,延长CE交AD于点F,由于∠DAB与∠ADB互余,从而∠ECB也与∠ADB互余,从而得征;
(3)方法与(2)相同;
(1)∵∠ABC=∠EBD,
∴∠ABC﹣∠ABE=∠EBD﹣∠ABE即∠EBC=∠DBA,
在△EBC和△DBA中,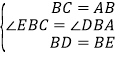 ,
,
∴△EBC≌△DBA,∴AD=EC,∠ECB=∠DAB.
∵∠ECB+∠ACE+∠CAB=90°,
∴∠DAB+∠ACE+∠CAB=90°,
∴∠AKC=90°,∴AD⊥EC.
(2)成立.理由如下:
如图3,延长CE交AD于F.
在△EBC和△DBA中, ,
,
∴△EBC≌△DBA,∴AD=EC,∠ECB=∠DAB.
∵∠DAB+∠ADB=90°,∴∠ECB+∠ADB=90°,∴AD⊥EC;
(3)AD=EC,AD⊥EC.理由如下:
如图4,设CE、AD交于点F,
∵∠DBE=∠ABC=90°,∴∠CBE=∠ABD.
在△EBC和△DBA中, ,
,
∴△EBC≌△DBA,∴AD=EC,∠CEB=∠ADB.
∵∠ADB+∠DFB=90°,∴∠CEB+∠AFE=90°,∴AD⊥EC.


 小学课时特训系列答案
小学课时特训系列答案