题目内容
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+ ![]() 与y轴相交于点A,点B与点O关于点A对称.
与y轴相交于点A,点B与点O关于点A对称. 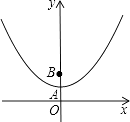
(1)填空:点B的坐标为;
(2)过点B的直线y=kx+b(其中k<0)与x轴相交于点C,过点C作直线l平行于y轴,P是直线l上一点,且PB=PC,求线段PB的长(用含k的式子表示),并判断点P是否在抛物线上,说明理由.
【答案】
(1)(0, ![]() )
)
(2)解:∵B点坐标为(0, ![]() ),
),
∴直线解析式为y=kx+ ![]() ,
,
解得:x=﹣ ![]() .
.
∴OC=﹣ ![]() .
.
∵PB=PC,
∴点P只能在x轴上方,
如图,过点B作BD⊥l于点D,设PB=PC=m,
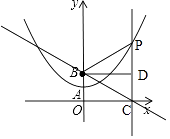
则BD=OC=﹣ ![]() ,CD=OB=
,CD=OB= ![]() ,
,
∴PD=PC﹣CD=m﹣ ![]() ,
,
在Rt△PBD中,由勾股定理可得PB2=PD2+BD2,即m2=(m﹣ ![]() )2+(﹣
)2+(﹣ ![]() )2,
)2,
解得:m= ![]() +
+ ![]() .
.
∴PB= ![]() +
+ ![]() .
.
∴点P坐标为(﹣ ![]() ,
, ![]() +
+ ![]() ).
).
当x=﹣ ![]() 时,代入抛物线解析式可得:y=
时,代入抛物线解析式可得:y= ![]() +
+ ![]() ,
,
∴点P在抛物线上.
【解析】解:(1)∵y=﹣x2+ ![]() 的顶点A的坐标为(0,
的顶点A的坐标为(0, ![]() ), ∴原点O关于点A的对称点B的坐标为(0,
), ∴原点O关于点A的对称点B的坐标为(0, ![]() ),
),
所以答案是:(0, ![]() );
);
【考点精析】关于本题考查的抛物线与坐标轴的交点,需要了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目