题目内容
【题目】已知:AB,PQ是圆O的两条直径,连接PB,AQ.
(1)如图①,求证:AQ∥BP,AG∥BP; 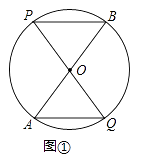
(2)如图②,过点B作BC⊥PQ于点D,交圆O于点C,在DG上取一点K,使DK=DP,求证:四边形AQKC是平行四边形. 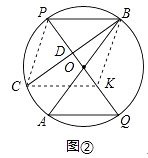
【答案】
(1)证明:∵ ![]() =
= ![]() ,
,
∴∠P=∠A,
∵OA=OQ,
∴∠A=∠Q,
∴∠P=∠Q,
∴AQ∥PB.
∵∠AOQ=∠BOP,
∴ ![]() =
= ![]() ,
,
∴AQ=BP;
(2)证明:∵PQ⊥BC,
∴BD=CD,
又∵PD=DK,
∴BC与PK互相垂直且平分,
∴四边形BKCP为菱形;
∴PB∥CK,且PB=CK,
∵PB∥AQ,
∴CK∥AQ,
∵PB=AQ,
∴CK=AQ,
∵CK∥AQ,且CK=AQ,
∴四边形AQKC为平行四边形.
【解析】(1)由同弧所对的圆周角相等得出∠P=∠A,由OA=OQ得出∠A=∠Q,那么∠P=∠Q,AQ∥PB.根据∠AOQ=∠BOP,得到 ![]() =
= ![]() ,那么AQ=BP;(2)先由垂径定理得出BD=CD,又PD=DK,得出四边形BKCP为菱形,根据菱形的性质得出PB∥CK,再证明CK∥AQ,且CK=AQ,那么四边形AQKC为平行四边形.
,那么AQ=BP;(2)先由垂径定理得出BD=CD,又PD=DK,得出四边形BKCP为菱形,根据菱形的性质得出PB∥CK,再证明CK∥AQ,且CK=AQ,那么四边形AQKC为平行四边形.
【考点精析】本题主要考查了平行四边形的判定和圆周角定理的相关知识点,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.

练习册系列答案
相关题目