题目内容
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的点,
上的点,![]() 且
且![]() 与
与![]() 之间的距离为4,则
之间的距离为4,则![]() 的长为( )
的长为( )

A. 3B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
过点D作DG⊥BE,垂足为G,则GD=4=AB,∠G=90°,再利用AAS证明△AEB≌△GED,根据全等三角形的性质可得AE=EG. 设AE=EG=x,则ED=5﹣x,在Rt△DEG中,由勾股定理得可得方程x2+42=(5﹣x)2, 解方程求得x的值即可得AE的长.
过点D作DG⊥BE,垂足为G,如图所示:

则GD=4=AB,∠G=90°,
∵四边形ABCD是矩形,
∴AD=BC=5,∠A=90°=∠G,
在△AEB和△GED中,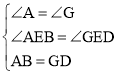
∴△AEB≌△GED(AAS).
∴AE=EG.
设AE=EG=x,则ED=5﹣x,
在Rt△DEG中,由勾股定理得:ED2=EG2+GD2,
∴x2+42=(5﹣x)2,
解得:x=![]() ,即AE=
,即AE=![]() .
.
故选D.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
【题目】如图,有一个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.

(1)填写下表;
层数 | 1 | 2 | 3 | 4 | 5 | … |
该层对应的点数 | 1 | 6 | __________ | __________ | __________ | … |
(2)写出第![]() 层所对应的点数;
层所对应的点数;
(3)是否存在![]() ,使得第
,使得第![]() 层有96个点?如果存在,求出
层有96个点?如果存在,求出![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.




