题目内容
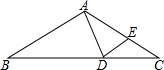
在△ABC中，∠ACB=90°，点D、E都在AB上，且AD=AC，BC=BE，求∠DCE的度数．
∵AD=AC，BC=BE，
∴∠ACD=∠ADC，∠BCE=∠BEC，
∴∠ACD=（180°-∠A）÷2①，∠BCE=（180°-∠B）÷2②，
∵∠A+∠B=90°，
∴①+②-∠DCE得，∠ACD+∠BCE-∠DCE=180°-（∠A+∠B）÷2-∠DCE=180°-45°-∠DCE=135°-∠DCE=90°，
∴∠DCE=45°．
∴∠ACD=∠ADC，∠BCE=∠BEC，
∴∠ACD=（180°-∠A）÷2①，∠BCE=（180°-∠B）÷2②，
∵∠A+∠B=90°，
∴①+②-∠DCE得，∠ACD+∠BCE-∠DCE=180°-（∠A+∠B）÷2-∠DCE=180°-45°-∠DCE=135°-∠DCE=90°，
∴∠DCE=45°．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
