题目内容
如图，点D在等腰△ABC底边BC上，且AB=BD，E是AC上一点，且AE=AD，∠DAE=30°，则∠B=（ ）
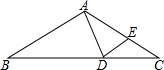
| A．30° | B．40° | C．45° | D．50° |
∠B+∠C+∠BAD+∠DAE=180°
∵AB=BD，
∴∠BAD=∠BDA．
∵AE=AD，
∴∠ADE=∠AED，
∵∠DAE=30°，
∴∠B+∠B+
（180°-∠B）+30°=180°，
∴∠B=40°．
故选B．
∵AB=BD，
∴∠BAD=∠BDA．
∵AE=AD，
∴∠ADE=∠AED，
∵∠DAE=30°，
∴∠B+∠B+
| 1 |
| 2 |
∴∠B=40°．
故选B．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
