Question

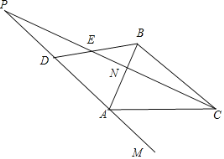
【题目】如图，已知△ABC，∠A＝∠B＝70°．请按如下要求操作并解答：

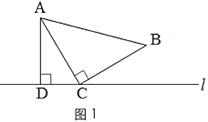
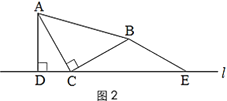
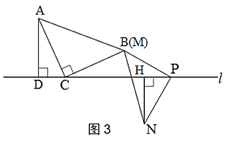
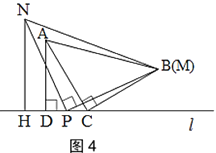
（1）在图中，过点A画直线MP∥BC，过点C画直线NP⊥AB，直线MP与NP交于点P，求∠APC的度数；

（2）在（1）的前提下，直线PM上存在点D，且∠ABD＝∠ADB，求直线BD与直线PN相交所形成的锐角的度数．

Answer 1

【答案】（1）∠APC＝20°；（2）直线BD与直线PN相交所形成的锐角的度数为35°．

【解析】

（1） 先作图，再根据内错角定理即可求出∠APC的度数.

（2） 根据MP∥BC可得∠ADB+∠CBD，再求得∠ABD＝∠ADB＝55，∠BEN＝90°-∠BNE即可解答

解：（1）如图所示，∵PC⊥AB，

∴∠CNB＝90°，

∵∠ABC＝70°，

∴∠BCN＝20°，

∵MP∥BC，

∴∠APC＝∠BCN＝20°；

（2）∵MP∥BC，

∴∠ADB+∠CBD＝180°，

∵∠ABD＝∠ADB，∠ABC＝70°，

∴∠ABD＝∠ADB＝55°，

∵∠BNE＝90°，

∴∠BEN＝90°﹣55°＝35°，

∴直线BD与直线PN相交所形成的锐角的度数为35°．