题目内容
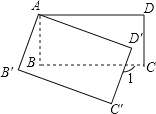
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小矩形,且m>n.(以上长度单位:cm)
(1)用含m,n的代数式表示所有裁剪线(图中虚线部分)的长度之和;
(2)观察图形,发现代数式2m2+5mn+2n2可以因式分解为 ;
(3)若每块小矩形的面积为10cm2,四个正方形的面积和为58cm2,试求(m+n)2的值.

【答案】(1)图中所有裁剪线(虚线部分)长度之和为6(m+n);(2)(m+2n)(2m+n);(3)(m+n)2=49.
【解析】
(1)根据整式的加减混合运算法则计算;
(2)根据图形的面积的不同的表示方法解答;
(3)变形完全平方公式,代入计算即可.
解:(1)图中所有裁剪线(虚线部分)长度之和为:2(m+2n)+2(2m+n)=6m+6n=6(m+n);
(2)2m2+5mn+2n2可以因式分解为:(m+2n)(2m+n),
故答案为:(m+2n)(2m+n);
(3)依题意得,2m2+2n2=58,mn=10,
∴m2+n2=29,
∵(m+n)2=m2+2mn+n2,
∴(m+n)2=29+20=49.

练习册系列答案
相关题目
【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?