题目内容
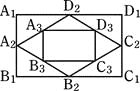
【题目】如图，矩形A1B1C1D1的面积为4，顺次连结各边中点得到四边形A2B2C2D2，再顺次连结四边形A2B2C2D2四边中点得到四边形A3B3C3D3，依此类推，则四边形AnBnCnDn的面积是 ．
【答案】
【解析】
∵四边形A1B1C1D1是矩形，
∴∠A1=∠B1=∠C1=∠D1=90°，A1B1=C1D1，B1C1=A1D1；
又∵各边中点是A2、B2、C2、D2，
∴四边形A2B2C2D2的面积=
=
×A1D1×A1B1×4
=矩形A1B1C1D1的面积，
即四边形A2B2C2D2的面积=矩形A1B1C1D1的面积；
同理，得
四边形A3B3C3D3=四边形A2B2C2D2的面积=
矩形A1B1C1D1的面积；
以此类推，四边形AnBnCnDn的面积=
矩形A1B1C1D1的面积=．
故答案是：．
练习册系列答案
相关题目
