题目内容
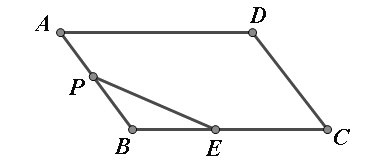
【题目】如图,平行四边形![]() 中,
中,![]() ,
,![]() ,∠
,∠![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 的边上,若
的边上,若![]() 为等腰三角形,则
为等腰三角形,则![]() 的长为__________.
的长为__________.
【答案】![]() 或
或![]() 或6
或6
【解析】
根据点P所在的线段分类讨论,再分析每种情况下![]() 腰的情况,然后利用直角三角形的性质和勾股定理分别求值即可.
腰的情况,然后利用直角三角形的性质和勾股定理分别求值即可.
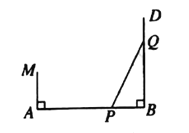
解:①当点P在AB上时,由∠ABC=120°,此时![]() 只能是以∠PBE为顶角的等腰三角形,BP=BE,过点B作BF⊥PE于点F,如下图所示
只能是以∠PBE为顶角的等腰三角形,BP=BE,过点B作BF⊥PE于点F,如下图所示

∴∠FBE=![]() ∠ABC=60°,EP=2EF
∠ABC=60°,EP=2EF
∴∠BEF=90°-∠FBE=30°
∵![]() ,点
,点![]() 是
是![]() 的中点
的中点
∴BE=![]()
在Rt△BEF中,BF=![]()
根据勾股定理:EF=![]()
∴EP=2EF=![]() ;
;
②当点P在AD上时,过点B作BF⊥AB于F,过点P作PG⊥BC,如下图所示
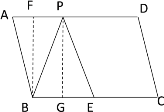
∵∠ABC=120°
∴∠A=60°
∴∠ABF=90°-∠A=30°
在Rt△ABF中AF=![]() ,BF=
,BF=![]()
∴BP≥BF>BE,EP≥BF>BE
∴此时![]() 只能是以∠BPE为顶角的等腰三角形,BP=PE,
只能是以∠BPE为顶角的等腰三角形,BP=PE,
∴PG=BF=![]() ,EG=
,EG=![]()
根据勾股定理:EP=![]() ;
;
③当点P在CD上时,过点E作EF⊥CD于F,过点B作BG⊥CD

由②可知:BE的中垂线与CD无交点,
∴此时BP≠PE
∵∠A=60°,四边形ABCD为平行四边形
∴∠C=60°
在Rt△BCG中,∠CBG=90°-∠C=30°,CG=![]()
根据勾股定理:BG=![]()
∴BP≥BG>BE
∵EF⊥CD,BG⊥CD,点E为BC的中点
∴EF为△BCG的中位线
∴EF=![]()
∴此时![]() 只能是以∠BEP为顶角的等腰三角形,BE=PE=6.
只能是以∠BEP为顶角的等腰三角形,BE=PE=6.
综上所述:![]() 的长为
的长为![]() 或
或![]() 或6.
或6.
故答案为:![]() 或
或![]() 或6
或6

 金钥匙试卷系列答案
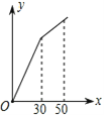
金钥匙试卷系列答案【题目】以下是某市自来水价格调整表(部分):(单位:元/立方米)
用水类别 | 现行水价 | 拟调整水价 |
一、居民生活用水 | 0.72 | |
1、一户一表 | ||
第一阶梯:月用水量0~30立方米/户 | 0.82 | |
第二阶梯:月用水量超过30立方米/户部分 | 1.23 |
则调整水价后某户居民月用水量x(立方米)与应交水费y(元)的函数图象是( )
A.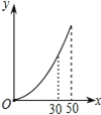 B.
B. C.
C. D.
D.