题目内容
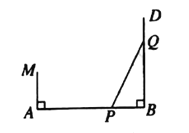
【题目】如图,![]() ,E为
,E为![]() 的中点,延长
的中点,延长![]() 交
交![]() 的延长线于点F,
的延长线于点F,![]() ,DC⊥BF.
,DC⊥BF.
(1)求证:![]() ;
;
(2)若![]() ,求证:
,求证:![]() 为等边三角形.
为等边三角形.
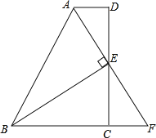
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据平行线的性质得出∠D=∠ECF,利用ASA证明△ADE与△FCE全等,再根据全等三角形的性质证明即可;
(2)根据等腰三角形的判定得出△ABF是等腰三角形,再由∠AED=∠CEF=30°,得出∠F=60°,进而证明△ABF是等边三角形.
证明:(1)![]() ,
,
![]() ,
,
![]() 为
为![]() 的中点,
的中点,
![]() ,
,
在![]() 与
与![]() 中
中
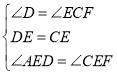 ,
,
![]() ≌
≌![]() ,
,
![]() ;
;
(2)![]() ,
,![]() ,
,
∴在△AEB和△BEF中
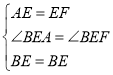 ,
,
∴△AEB≌△BEF(SAS),∴AB=BF,
即△ABF是等腰三角形,
∵∠AED=∠CEF=30°,∠ECF=90°,
∴∠F=60°,
∴△ABF是等边三角形.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
【题目】以下是某市自来水价格调整表(部分):(单位:元/立方米)
用水类别 | 现行水价 | 拟调整水价 |
一、居民生活用水 | 0.72 | |
1、一户一表 | ||
第一阶梯:月用水量0~30立方米/户 | 0.82 | |
第二阶梯:月用水量超过30立方米/户部分 | 1.23 |
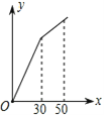
则调整水价后某户居民月用水量x(立方米)与应交水费y(元)的函数图象是( )
A.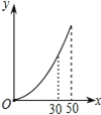 B.
B. C.
C.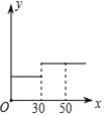 D.
D.