题目内容
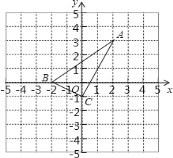
【题目】如图,直角坐标系中的网格由单位正方形构成,△ABC中,A点坐标为(2,3),B点坐标为(-2,0),C点坐标为(0,-1).
(1)AC的长为______;
(2)求证:AC⊥BC;
(3)若以A、B、C及点D为顶点的四边形为平行四边形ABCD,画出平行四边形ABCD,并写出D点的坐标______.
【答案】(1)![]() ;(2)证明见解析;(3)画图见解析,(0,4),(4,2),(-4,-4).
;(2)证明见解析;(3)画图见解析,(0,4),(4,2),(-4,-4).
【解析】
(1)根据A点与C点的坐标,应用两点间的距离公式求解即得;
(2)先根据两点的距离公式分别计算AC、AB和BC的长度的平方,在根据勾股定理逆定理证明即得;
(3)分别以AC、AB和BC为对角线即可画出平行四边形.
(1)解:∵A(2,3),C(0,-1)
∴AC=![]()
故答案为:![]() ;
;
(2)证明:∵A(2,3),B(-2,0),C(0,-1)
∴BC2=12+22=5,AB2=32+42=25,AC2=20,
∴BC2+AC2=AB2,
∴△ABC是直角三角形,
∵![]()
∴AC⊥BC;
(3)如图所示:
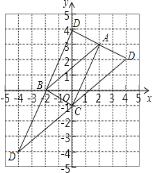
当AB为平行四边形对角线时,D点的坐标(0,4);
当AC为平行四边形对角线时,D点的坐标(4,2);
当BC为平行四边形对角线时,D点的坐标(-4,-4).
故答案为:(0,4),(4,2),(-4,-4).

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目