题目内容
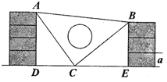
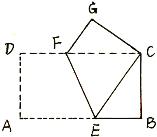
【题目】如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)试判断△CEF的形状,并证明你的结论;
(3)若AB=8,AD=4,求四边形ECGF的面积.
【答案】(1)证明见解析;(2)△CEF是等腰三角形;(3)16.
【解析】
(1)根据折叠性质,GC=AD=BC,∠G=∠D=∠B=90°.再证∠GCF=∠BCE,根据ASA判定全等;(2)根据(1)的结论即可直接判断;(3)由(1)可知,四边形ECGF的面积=四边形BCFE面积=矩形面积的一半.
(1)证明:∵四边形ABCD是矩形,
∴AD=BC,∠D=∠B=90°.
根据折叠的性质,有GC=AD,∠G=∠D.
∴GC=BC,∠G=∠B.
又∠GCF+∠ECF=90°,∠BCE+∠ECF=90°,
∴∠GCF=∠BCE.
∴△FGC≌△EBC(AAS);
(2)解:△CEF是等腰三角形.
∵△FGC≌△EBC
∴CE=CF,
即△CEF是等腰三角形.
(3)解:由(1)知,四边形ECGF的面积=四边形EADF的面积=四边形EBCF的面积=矩形ABCD的面积的一半.
∵AB=8,AD=4,
∴矩形ABCD的面积=8×4=32,
∴四边形ECGF的面积=16.
故答案为(1)证明见解析;(2)△CEF是等腰三角形;(3)16.

练习册系列答案
相关题目