题目内容
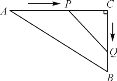
【题目】如图,在△ABC中,AC=50 cm,BC=40 cm,∠C=90°,点P从点A开始沿AC边向点C以2 cm/s的速度匀速移动,同时另一点Q从点C开始以3 cm/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300 cm2时,运动时间为__________.
【答案】5s
【解析】
设x秒后,△PCQ的面积等于300cm2,根据路程=速度×时间,可用时间x表示出CP和CQ的长,然后根据直角三角形的面积公式,得出方程,求出未知数,然后看看解是否符合题意,将不合题意的舍去,即可得出时间的值.
设x秒后,△PCQ的面积等于300cm2,有:![]() (50-2x)×3x=300,
(50-2x)×3x=300,
∴x2-25x+50=0,
∴x1=5,x2=20.
当x=20s时,CQ=3x=3×20=60>BC=40,即x=20s不合题意,舍去.
答:5秒后,△PCQ的面积等于300cm2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素含量C及购这两种原料的价格如下表:
甲 | 乙 | |
维生素C(单位/千克) | 600 | 100 |
原料价格(元/千克) | 8 | 4 |
现配制这种饮料10千克,要求至少含有4200单位的维生素C,并要求购买甲、乙两种原料的费用不超过72元.请问:既要符合要求又要成本最低,则购买甲种原料应该在什么范围之内,最低成本是多少元?