题目内容
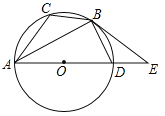
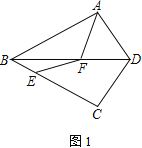
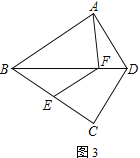
【题目】如图,△ABD、△CBD关于直线BD对称,点E是BC上一点,线段CE的垂直平分线交BD于点F,连接AF、EF.
(1) 求证:AF=EF;
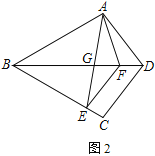
(2) 如图2,连接AE交BD于点G.若EF∥CD,求证:![]() ;
;
(3) 如图3,若∠BAD=90°,且点E在BF的垂直平分线上,tan∠ABD=![]() ,DF=
,DF=![]() ,请直接写出AF的长.
,请直接写出AF的长.
【答案】(1)CF=EF=AF(2)证明见解析(3)![]()
【解析】(1)如图1,连接CF,根据轴对称的性质和线段垂直平分线的性质证得结论;
(2)结合已知条件易证△ABD∽△EBF,则该相似三角形的对应边成比例:![]() =
=![]() ,即
,即![]() =
=![]() .然后由角平分线定理推知
.然后由角平分线定理推知![]() =
=![]() ,所以根据等量代换证得
,所以根据等量代换证得![]() =
=![]() ;
;
(3)如图3,过点E作EH⊥BD于H.结合锐角三角函数定义可以设EH=3a,BH=4a,则BE=EF=5a,BF=8a.过点F作FG⊥EC于G,在直角△GBF中,利用锐角三角函数定义求得线段FG、EG、BD的长度,则易得DF的长度,所以AF=EF=5a.
(1)如图1,连接CF.
∵△ABD、△CBD关于直线BD对称,线段CE的垂直平分线交BD于点F,∴CF=EF=AF,故AF=EF;
(2)由(1)可知:AF=EF.
∵△ABD、△CBD关于直线BD对称,∴△ABD≌△CBD.
又∵EF∥CD,∴△CBD∽△EBF,∴△ABD∽△EBF,∴![]() =
=![]() ,即
,即![]() =
=![]() .
.
又BD为∠ABC的平分线,∴![]() =
=![]() (角平分线定理),∴
(角平分线定理),∴![]() =
=![]() ;
;
(3)如图3,过点E作EH
∵tan∠EBH=tan∠ABD=![]() ,设EH=3a,BH=4a,则HE=3a,BE=EF=5a,BF=8a.
,设EH=3a,BH=4a,则HE=3a,BE=EF=5a,BF=8a.
过点F作FG⊥EC于G,∴tan∠GBF=![]() ,∴FG=
,∴FG=![]() a,EG=CG=
a,EG=CG=![]() a,BC=BE+EG+GC=5a+
a,BC=BE+EG+GC=5a+![]() a+
a+![]() a=
a=![]() ,BD=
,BD=![]() a,∴DF=
a,∴DF=![]() a﹣8a=
a﹣8a=![]() a=
a=![]() ,a=
,a=![]() ,∴AF=5a=
,∴AF=5a=![]() .
.
故答案为:![]() .
.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案