Question

【题目】如图，在矩形ABCD中，E，F为BC上两点，且BE=CF，连接AF，DE交于点O．求证：

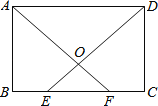
（1）△ABF≌△DCE；

（2）△AOD是等腰三角形．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

（1）根据矩形的性质可得∠B=∠C=90°，AB=DC，然后求出BF=CE，再利用“边角边”证明△ABF和△DCE全等即可.

（2）根据全等三角形对应角相等可得∠BAF=∠EDC，然后求出∠DAF=∠EDA，然后根据等腰三角形的定义证明即可.

（1）在矩形ABCD中，∠B=∠C=90°，AB=DC，

∵BE=CF，BF=BC﹣FC，CE=BC﹣BE，∴BF=CE.

在△ABF和△DCE中，∵AB=DC，∠B=∠C，BF=CE，

∴△ABF≌△DCE（SAS）.

（2）∵△ABF≌△DCE，∴∠BAF=∠EDC.

∵∠DAF=90°﹣∠BAF，∠EDA=90°﹣∠EDC，∴∠DAF=∠EDA.

∴△AOD是等腰三角形.