题目内容
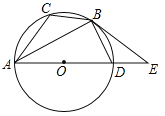
【题目】如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,BE是⊙O的切线,B是切点.
(1)求证:∠EBD=∠CAB;
(2)若BC=![]() ,AC=5,求sin∠CBA.
,AC=5,求sin∠CBA.
【答案】(1)见解析(2)![]()
【解析】(1)先根据等弦所对的劣弧相等,再由切线的性质和圆周角定理即可得出结论;
(2)利用三角形的中位线先求出OF,再用勾股定理求出半径R.在Rt△ODF中,求出sin∠ODF的值,即可得出结论.
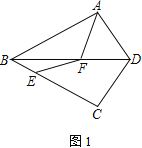
如图1,连接OB.
∵BD=BC,∴∠CAB=∠BAD.
∵BE是⊙O的切线,∴∠EBD+∠OBD=90°.
∵AD是⊙O的直径,∴∠ABD=90°,OA=BO,∴∠BAD=∠ABO,∴∠EBD=∠BAD.
∵BD=BC,∴∠CAB=∠DAB,∴∠EBD=∠CAB.

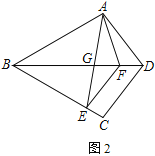
(2)如图2,设圆的半径为R,连接CD.
∵AD为⊙O的直径,∴∠ACD=90°.
∵BC=BD,∴OB⊥CD,∴OB∥AC.
∵OA=OD,∴OF=![]() AC=2.5,∴BF=R-2.5,FD2=OD2-OF2= R2-2.52
AC=2.5,∴BF=R-2.5,FD2=OD2-OF2= R2-2.52
在Rt△BFD中,∵BF2+FD2=BD2,∴![]() ,2R2-5R-3=0,
,2R2-5R-3=0,
∴(2R+1)(R-3)=0.
∵R>0,∴R=3.
在Rt△ODF中,sin∠ODF=![]() =
=![]() =
=![]() .
.
∵∠CBA=∠CDA,∴sin∠CBA=sin∠CDA= sin∠ODF=![]() .
.


练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目