Question

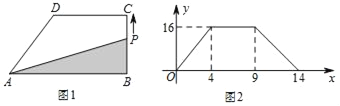
【题目】根据图①所示的程序，得到了如图②y与x的函数图像，若点M是y轴正半轴上任意一点，过点M作PQ∥x轴交图像于点P、Q，连接OP、OQ.则以下结论：

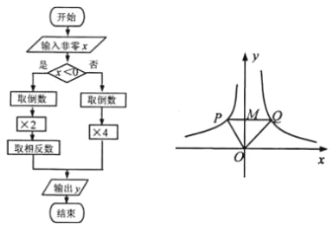
①x<0时，y=； ②△OPQ的面积为定值； ③x>0时，y随x的增大而增大；

④MQ=2PM; ⑤∠POQ可以等于90°.

其中正确结论序号是

A. ①②③ B. ②③④ C. ③④⑤ D. ②④⑤

Answer 1

【答案】D

【解析】

由流程图可知函数解析式从而判断①；S△OPQ= S△PMQ+ S△MQO=1+2=3，可判断②；由图像可判断③；由流程图可知函数解析式：x＜0时，y=；x＞0时，y=，再分别用OM表示PM和MQ即可证明；∠POQ=90°时，△PMO∽△OMQ，利用相似的性质可求解出PM、QM以及OM三者之间的关系，即PM、QM以及OM三者之间满足一定的数量关系可得到∠POQ=90°，据此判断⑤.

解：由流程图可知，x＜0时，y=，故①错误；由反比例函数系数k的几何意义可得S△PMQ =1，S△MQO=2，则S△OPQ= S△PMQ+ S△MQO=1+2=3，故②正确；由图像可知，x＞0时，y随x的增大而减小，故③错误；由流程图可知函数解析式：x＜0时，y=；x＞0时，y=，则PM=，MQ=，则MQ=2PM，故④正确；∠POQ=90°时，△PMO∽△OMQ，则，则可得OM2=PM×MQ，即当OM2=PM×MQ时，∠POQ=90°，故⑤正确.

故选择D.