题目内容
【题目】Rt△ABC中,∠C=90°,AC=6,BC=8,D是AB的中点,E、F分别是AC、BC上两点,且ED⊥FD.
(1)如图1,若E是AC中点,则BF=______,EF=______,AE2+BF2______EF2(填“>,<或=”);
(2)如图2,若点E是AC边上任意一点,AE2+BF2_____EF2(填“>,<或=”),请说明理由;
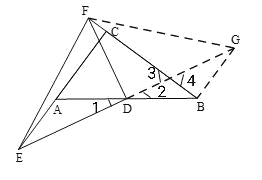
(3)若点E在CA延长上,(2)中三条线段之间的关系是否成立?请画图说明.



【答案】(1)4;5;=;(2)=;证明见解析;(3)见解析.
【解析】
(1)由∠C=90°,AC=6,BC=8,可得![]() ,
,
又因为E是AC的中点,D是AB的中点,可得![]() ,所以∠DEF=∠CFE,因为ED⊥FD,所以∠EDF=90°,即∠CEF+∠CFE=∠DFE+∠DEF=90°,推出∠DFE=∠CEF,得到DF∥AC,又因为D为AB中点,推出F是BC的中点,所以
,所以∠DEF=∠CFE,因为ED⊥FD,所以∠EDF=90°,即∠CEF+∠CFE=∠DFE+∠DEF=90°,推出∠DFE=∠CEF,得到DF∥AC,又因为D为AB中点,推出F是BC的中点,所以![]() ,因为E是AC的中点,F为BC中点,所以
,因为E是AC的中点,F为BC中点,所以![]() ,由勾股定理得
,由勾股定理得![]() ,等量替代即可得到
,等量替代即可得到![]() ;
;
(2)如图,延长ED至G使得ED =DG,连接BG,FG,因为D是AB的中点,可得AD=BD,通过证△ADE≌△BDG,可得AE=BG,∠A=∠3,又∠C =90°,所以∠A+∠ABC=90°,所以∠3+∠ABC=∠FBG=90°,可得BG2+BF2=FG2,因为AE=BG,所以AE2+BF2=FG2,因为DE=DG,∠EDF=90°,所以FE=FG,即可推出AE2+BF2=EF2;
(3)成立,延长ED至G使得ED=DG,连接BG,FG,因为D是AB的中点,可得AD=BD,因为∠1=∠2,DE=DG,得到△ADE≌△BDG,所以AE=BG,∠AED=∠BGD,因为∠3=∠4,∠AED=∠BGD,推出∠GBF=∠C=90°,因为FD⊥ED,D为EG中点,所以EF=FG,又在Rt△BFG中,BG2+BF2=FG2,等量替代可得AE2+BF2=EF2;
解:(1)∵∠C=90°,AC=6,BC=8,
∴![]() ,
,
∵E是AC的中点,D是AB的中点,
∴![]() ,
,
∴∠DEF=∠CFE,
∵ED⊥FD,
∴∠EDF=90°,
∴∠CEF+∠CFE=∠DFE+∠DEF=90°,
∴∠DFE=∠CEF,
∴DF∥AC,
∵D为AB中点,
∴F为BC中点,
∴![]() ,
,
∵E是AC的中点,F为BC中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
故答案为:4; 5;AE2+BF2=EF2;
(2)AE2+BF2=EF2,
如图,延长ED至G使得ED=DG,连接BG,FG.
∵D是AB的中点,
∴AD=BD,
∵∠1=∠2,DE=DG,
∴△ADE≌△BDG,
∴AE=BG,∠A=∠3,
∵∠C =90°,
∴∠A+∠ABC=90°,
∴∠3+∠ABC=∠FBG=90°,
∴BG2+BF2=FG2,
∵AE=BG,
∴AE2+BF2=FG2,
∵DE=DG,∠EDF=90°,
∴FE=FG,
∴AE2+BF2=EF2,

(3)成立,如图,延长ED至G使得ED=DG,连接BG,FG,
∵D是AB的中点,
∴AD=BD,
∵∠1=∠2,DE=DG,
∴△ADE≌△BDG,
∴AE=BG,∠AED=∠BGD,
∵∠3=∠4,∠AED=∠BGD,
∴∠GBF=∠C=90°,
∵FD⊥ED,D为EG中点,
∴EF=FG,
在Rt△BFG中,BG2+BF2=FG2,
即AE2+BF2=EF2;