题目内容
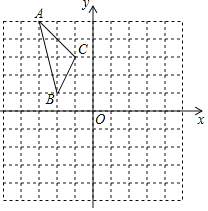
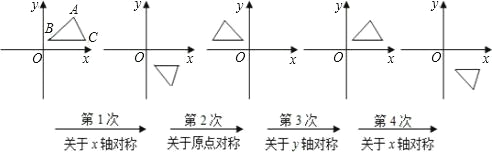
【题目】如图，在平面直角坐标系中，对△ABC 进行循环往复的轴对称或中心对称变换，若原来点 A 坐标是(a，b)，则经过第 2012 次变换后所得的 A 点坐标是( )
A. (a，b) B. (a，﹣b) C. (﹣a，b) D. (﹣a，﹣b)
【答案】C
【解析】
观察图形不难发现，每三次变换为一个循环组循环，用2012除以3，根据余数的情况确定最后点A所在的象限，然后根据关于坐标轴对称的点的变化规律解答．
由图可知，经过3次对称变换后△ABC又回到原来位置，
∵2012÷3=670…2，
∴第2012次变换后所得的A点与第2次变换后的点A的位置相同，
即与原图形关于y轴对称，
∵点A坐标是（a，b），
∴第2012次变换后所得的A点坐标（-a，b）．
故选C．
练习册系列答案
相关题目
